Правила настройки

Настройка параметров (обучение) персептрона осуществляется с использованием обучающего множества. Обозначим через p вектор входов персептрона, а через t – вектор соответствующих желаемых выходов. Цель обучения – уменьшить погрешность e = a – t, которая равна разности между реакцией нейрона a и вектором цели t.

Правило настройки (обучения) персептрона должно зависеть от величины погрешности e. Вектор цели t может включать только значения 0 и 1, поскольку персептрон
с функцией активации hardlim может генерировать только такие значения.

При настройке параметров персептрона без смещения и с единственным нейроном возможны только 3 ситуации:

1. Для данного вектора входа выход персептрона правильный (a = t и e = t – а = 0) и тогда вектор весов w не претерпевает изменений.

2. Выход персептрона равен 0, а должен быть равен 1 (a = 0, t = 1 и e = t – 0 = 1). В этом случае вход функции активации w ^Т p отрицательный и его необходимо скорректировать. Добавим к вектору весов w вектор входа p, и тогда произведение (w ^T + p ^T) p =
= w ^T p + p ^T p изменится на положительную величину, а после нескольких таких шагов вход функции активации станет положительным и вектор входа будет классифицирован правильно. При этом изменятся настройки весов.

3. Выход нейрона равен 1, а должен быть равен 0 (а = 0, t = 1 и e = t – a = –1). В этом случае вход функции активации w ^Т p положительный и его необходимо скорректировать. Вычтем из вектора весов w вектор входа p, и тогда произведение (w ^T – p ^T) p =
= w ^T p – p ^T p изменится на отрицательную величину, а после нескольких шагов вход функции активации станет отрицательным и вектор входа будет классифицирован правильно. При этом изменятся настройки весов.

Теперь правило настройки (обучения) персептрона можно записать, связав изменение вектора весов D w с погрешностью e = t – a:

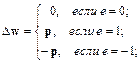(4.4а)

Все 3 случая можно описать одним соотношением:

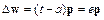. (4.4б)

Можно получить аналогичное выражение для изменения смещения, учитывая, что смещение можно рассматривать как вес для единичного входа:

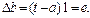(4.5)

В случае нескольких нейронов эти соотношения обобщаются следующим образом:

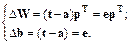(4.6)

Тогда правило настройки (обучения) персептрона можно записать в следующей форме:

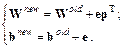(4.7)

Описанные соотношения положены в основу алгоритма настройки параметров персептрона, который реализован в ППП Neural Network Toolbox в виде М-функции learnp. Каждый раз при выполнении функции learnp будет происходить перенастройка параметров персептрона. Доказано, что если решение существует, то процесс обучения персептрона сходится за конечное число итераций. Если смещение не используется, функция learnp ищет решение, изменяя только вектор весов w. Это приводит к нахождению разделяющей линии, перпендикулярной вектору w и которая должным образом разделяет векторы входа.

Рассмотрим простой пример персептрона с единственным нейроном и двухэлементным вектором входа:

net = newp([–2 2;–2 2],1);

Определим смещение b равным 0, а вектор весов w равным [1 –0.8]:

net.b{1} = 0;

w = [1 –0.8];

net.IW{1,1} = w;

Обучающее множество зададим следующим образом:

p = [1; 2];

t = [1];

Моделируя персептрон, рассчитаем выход и ошибку на первом шаге настройки (обучения):

a = sim(net,p)

a = 0

e = t–a

e = 1

Наконец, используя М-функцию настройки параметров learnp, найдем требуемое
изменение весов:

dw = learnp(w,p,[ ],[ ],[ ],[ ],e,[ ],[ ],[ ])

dw = 1 2

Тогда новый вектор весов примет вид:

w = w + dw

w = 2.0000 1.2000

Заметим, что описанные выше правило и алгоритм настройки (обучения) персептрона гарантируют сходимость за конечное число шагов для всех задач, которые могут быть решены с использованием персептрона. Это в первую очередь задачи классификации векторов, которые относятся к классу линейно отделимых,когда все пространство входов можно разделить на 2 области некоторой прямой линией, в многомерном случае – гиперплоскостью.

Демонстрационный пример nnd4pr позволяет выполнить многочисленные эксперименты по настройке (обучению) персептрона для решения задачи классификации входных векторов.