2015-08-21
552
Вообще говоря, можно ожидать, что всевозможные отклонения от максвелловского распределения, в частности течения плазмы, могут приводить к неустойчивостям. В ловушках для удержания плазмы всегда имеются градиенты плотности и температуры, что вызывает течение плазмы. В этом разделе мы рассмотрим одну из таких неустойчивостей в столкновительном режиме. Она не способна разрушить плазменный шнур, так как локализована вблизи рациональной поверхности, но может дать вклад в аномальный перенос (см. также раздел 3.6).
Рассмотрим плоскийслойплазмы в однородном магнитном поле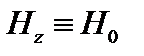 
, направленном вдоль оси z. В равновесии градиент давления направлен вдоль оси x. Скоростью частиц поперек магнитного поля, связанной с диффузией, и инерцией электронов можно пренебречь. Пренебрежем также стационарным электрическим полем и положим температуру ионов равной нулю. Тогда
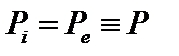, (4.2.1)
а ток имеет только полоидальную составляющую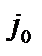 
. В нулевом приближении имеем
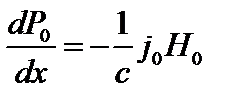. (4.2.2)
Мы будем рассматривать чисто электростатические возмущения, то есть пренебрегать возмущениями магнитного поля. Тогда уравнение движения плазмы приобретает вид
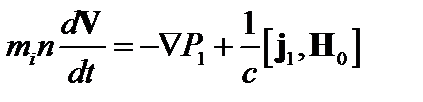. (4.2.3)
Обобщенный закон Ома дается выражением (5.4.6) [8]:
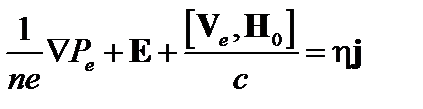. (4.2.4)
Здесь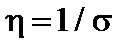 
– удельное сопротивление. Мы пренебрегли термосилой и вязкостью. С учётом соотношений 
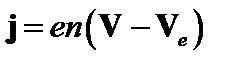и (4.2.1) можно написать:
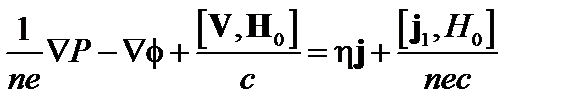. (4.2.5)
Мы ввели скалярный потенциал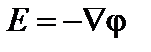 
. Кроме того, нам понадобятся уравнения непрерывности для вещества и электрического тока:
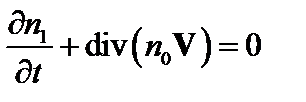(4.2.6)
и
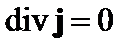. (4.2.7)
В фурье-представлении по времени уравнения (4.2.3) и (4.2.5) выглядят так:
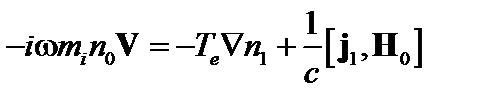; (4.2.8)
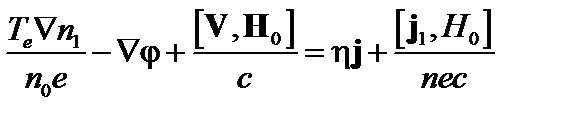. (4.2.9)
Выразим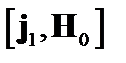 
из уравнения (4.2.9) и подставим в (4.2.8):
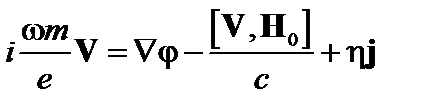. (4.2.10)
Все параметры равновесного состояния не зависят ни от y, ни от z. Поэтому возмущённые параметры можно разложить в интеграл Фурье по y и z. Тогда z -компоненту тока можно найти из уравнения (4.2.9):
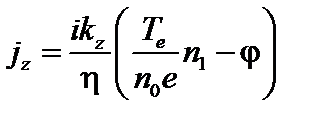. (4.2.11)
В уравнения (4.2.10) можно опустить член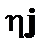 
. Соответствующие компоненты этого уравнения имеют вид
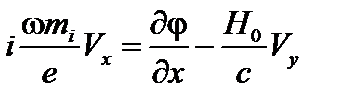(4.2.12)
и
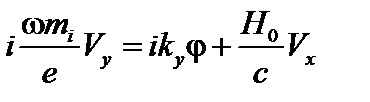. (4.2.13)
Разрешая эти два уравнения относительно Vx и Vy, получаем
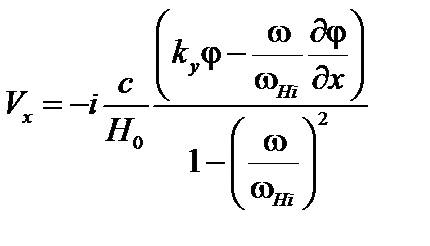; (4.2.14)
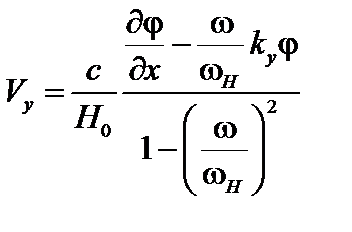. (4.2.15)
Здесь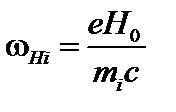 
– ионная циклотронная частота. Для дрейфовой диссипативной моды можно положить 
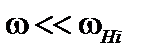. Поэтому членами, квадратичными по 
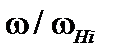, можно пренебречь,
Найдём теперь остальные компоненты возмущённого тока. Перпендикулярная составляющая уравнения (4.2.9) при пренебрежении членом, пропорциональным сопротивлению плазмы, даёт
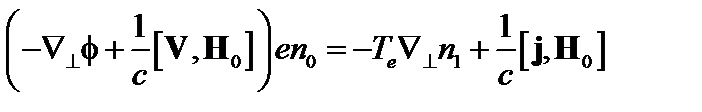, (4.2.16)
что в компонентах приобретает вид
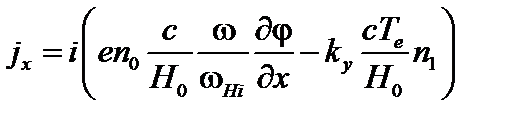; (4.2.17)
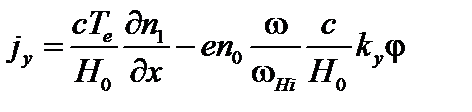. (4.2.18)
Подставим выражения для тока в уравнение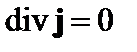 
и будем считать, что 
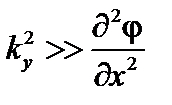. В результате получим
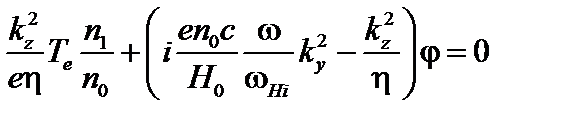. (4.2.19)
Ещё одно уравнение получим с помощью уравнения непрерывности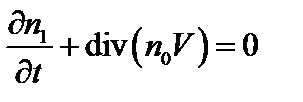 
. Из z -компоненты уравнения (4.2.8) находим
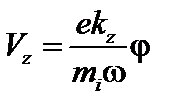. (4.2.20)
Подставляя (4.2.14), (4.2.15) и (4.2.20) в уравнение непрерывности, получаем
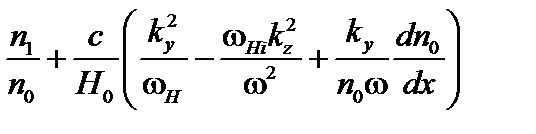. (4.2.21)
Определитель системы уравнений (4.2.19) и (4.2.21) даёт дисперсионное уравнение для дрейфовой диссипативной моды:
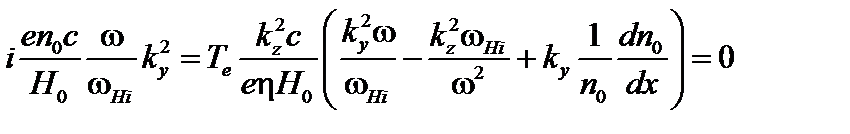(4.2.22)
или
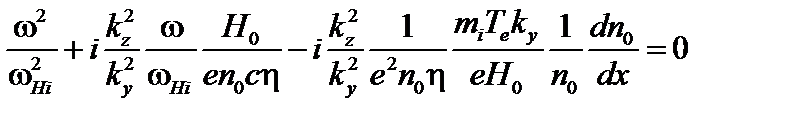. (4.2.23)
Это выражение можно представить также в виде
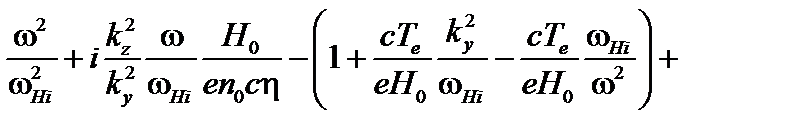
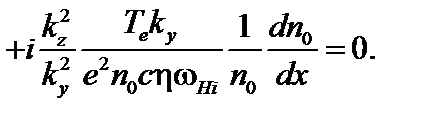(4.2.24)
В этом выражении в скобках можно пренебречь двумя последними членами по сравнению с единицей.
Введем дрейфовую частоту
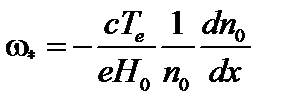. (4.2.25)
Умножим уравнение (4.2.24) на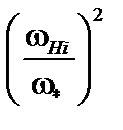 
. В результате дисперсионное уравнение приобретает вид
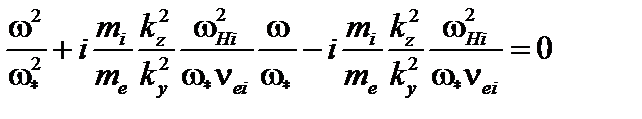. (4.2.26)
Введём безразмерную частоту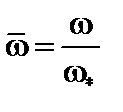 
и обозначение 
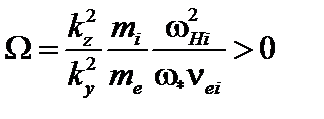. Тогда дисперсионное уравнение принимает совсем простой вид:
, 
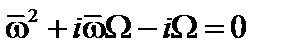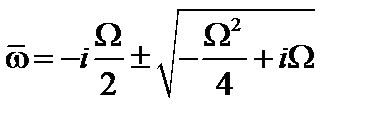. (4.2.27)
Рассмотрим случай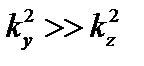 
. Для таких возмущений 
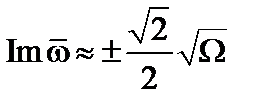или в размерном виде
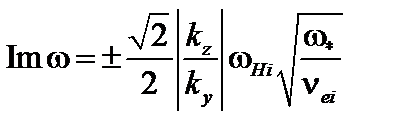. (4.2.28)
Как видно, решение со знаком «плюс» соответствует неустойчивости.
В противоположном случае,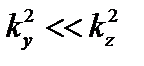 
получаем
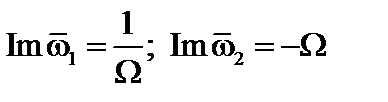, (4.2.29)
то есть одно из решений устойчиво, а другое слабо, неустойчиво.
