Неоклассическая теория переноса

В тороидальном случае классическая теория претерпевает существенные изменения, которые радикальным образом зависят от частоты столкновений. Рассмотрим сначала так называемый банановый режим.

Банановый режим

Это случай, когда обратная частота столкновений много больше периода обращения запертых частиц по банану ([8]).

Смещение пролётных частиц по радиусу мало отличается от ларморовского радиуса. Запертые частицы смещаются по радиусу на существенно большее расстояние:

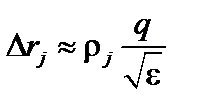. (5.2.1)

И хотя этих частиц в 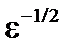раз меньше, их вклад в переносы оказывается определяющим.

Меняется также и эффективное время между столкновениями. В классическом случае это время, за которое скорость частицы в результате множества далеких столкновений повернётся в среднем на угол порядка 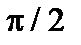. При этом она сместится на величину порядка ларморовского радиуса. В тороидальном случае пролётная частица, превратившись в запертую, сместится на величину порядка 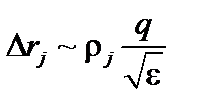. Запертая частица превращается в пролётную, если её скорость, первоначально направленная почти поперёк магнитного поля, должна повернуться на угол порядка 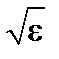. Случайное рассеяние на малые углы в результате столкновений аналогично броуновскому движению, когда средний квадрат смещения пропорционален времени, 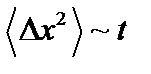. Аналогичное соотношение можно написать и для угла поворота скорости частицы:

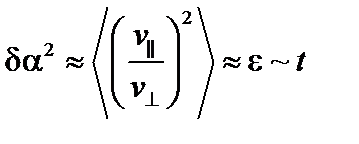. (5.2.2)

Таким образом, отношение этого времени к классическому составляет величину порядка, то есть

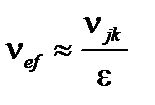. (5.2.3)

Кроме того, число запертых частиц в 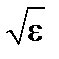раз меньше, чем полное число частиц. Таким образом, поток частиц поперек магнитного поля, определяется выражением

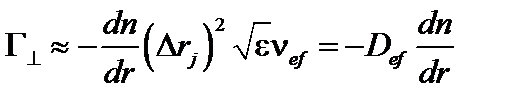, (5.2.4)

Здесь 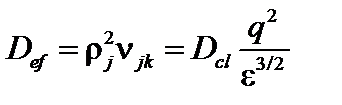, 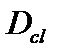– классический коэффициент диффузии.

Эта формула справедлива, если частица между столкновениями успевает совершить один или несколько полных оборотов по банановой траектории, прежде чем перейдет из запертых в пролётные, то есть

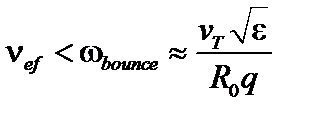
или

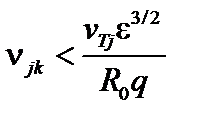. (5.2.5)

C ростом частоты столкновений плазма токамака переходит в «режим плато».

Режим плато

Этот режим реализуется при промежуточных частотах столкновений,

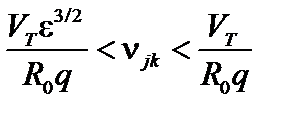. (5.2.6)

В этой области время между столкновениями уже меньше времени, за которое запертая частица обходит банан, но больше, чем время, за которое пролётная частица обходит тор по тороидальному направлению.

Для нахождения коэффициента диффузии в этой области воспользуемся стационарным кинетическим уравнением в 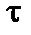-приближении.

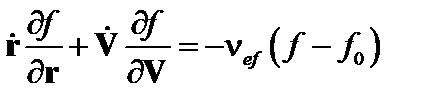. (5.2.7)

Скорость можно представить как сумму продольной скорости и поперечной дрейфовой скорости:

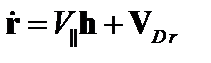. (5.2.8)

Дрейфовую скорость можно считать много меньше параллельной, .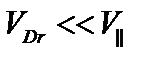

Функцию распределения можно представить как сумму цилиндрически симметричной части и малой добавки, зависящей от полоидального угла.

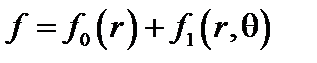. (5.2.9)

В нулевом приближении имеем , .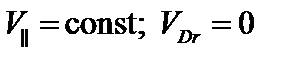

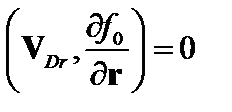В первом приближении

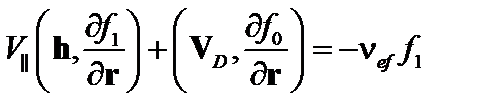. (5.2.10)

Напомним, что магнитное поле в токамаке с круглыми магнитными поверхностями не имеет радиальной компоненты и не зависит от тороидальной координаты, .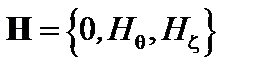

Первый член в уравнении (5.2.10) можно преобразовать так:

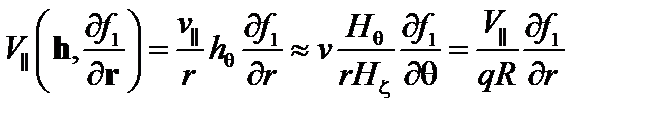. (5.2.11)

Рассмотрим второй член в уравнении (5.2.10). Основной дрейф определяется градиентом поля

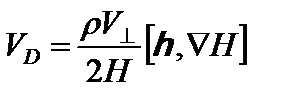Направлен этот дрейф вдоль оси симметрии тора. Радиальная компонента его скорости определяется выражением

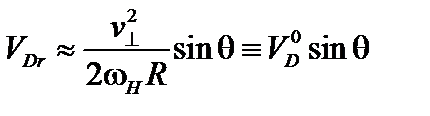. (5.2.12)

Подставим (5.2.11) и (5.2.12) в (5.2.10). В результате получаем

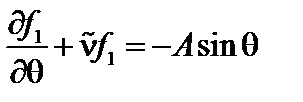. (5.2.13)

Здесь 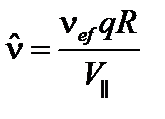; 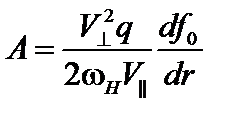. Решение этого уравнения имеет вид

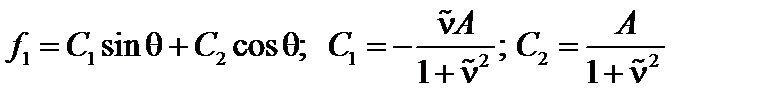. (5.2.14)

Теперь нетрудно вычислить радиальный поток частиц:

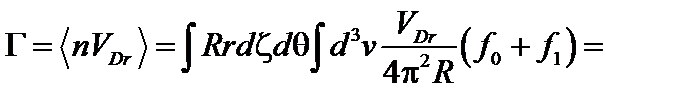
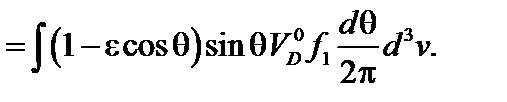(5.2.15)

При интегрировании по 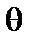обратился в ноль. Обращаются также в ноль члены, пропорциональные , , .

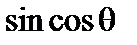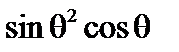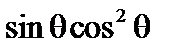В результате получаем

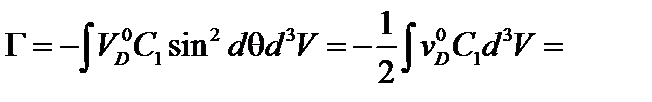
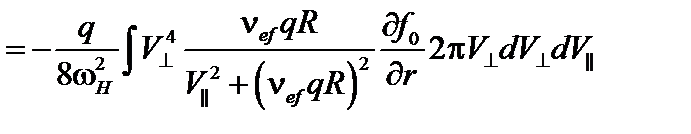. (5.2.16)

При малых частотах столкновений этот интеграл можно преобразовать с помощью соотношения, известного из теории обобщенных функций:

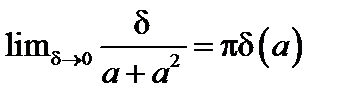. (5.2.17)

Используя это соотношение и подставляя вместо 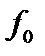максвелловскую функцию 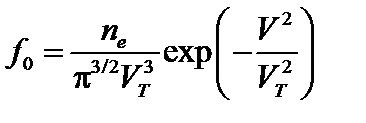, получаем

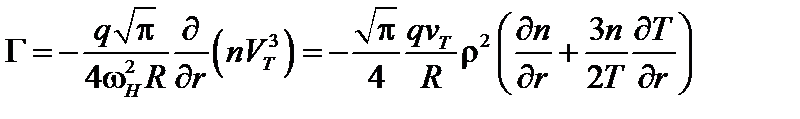. (5.2.18)

Таким образом, в области плато коэффициенты диффузии и теплопроводности не зависят от частоты столкновений,

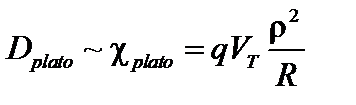. (5.2.19)

Заметим, что, в отличие от классической диффузии, коэффициент диффузии в области плато неодинаков для электронов и ионов, поэтому скорость диффузии будет определяться наименьшим из электронного и ионного коэффициентов. Это не относится к коэффициенту теплопроводности. Поэтому перенос тепла по ионному каналу будет существенно выше переноса тепла по электронному.

Режим Пфирш–Шлютера.

При увеличении частоты столкновений плазма переходит в гидродинамический режим, так называемый режим Пфирша–Шлютера. В этом режиме столкновения приводят к тому, что исчезает разница между запертыми и пролетными частицами. Параллельная скорость у частиц имеет порядок тепловой скорости и слабо зависит от полоидального угла. Смещение частицы от магнитной поверхности при этом составляет в среднем величину 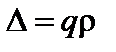([8], (3.20)). Тогда коэффициент диффузии можно оценить по обычной формуле:

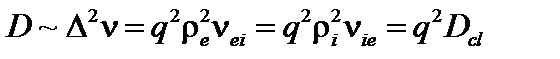. (5.2.20)

Эта величина в 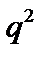раз больше классической величины и не зависит от сорта частиц. Таким образом, в режиме Пфирша–Шлютера диффузия снова оказывается автоматически амбиполярной.

Характер коэффициента переноса показан на рис. 12.

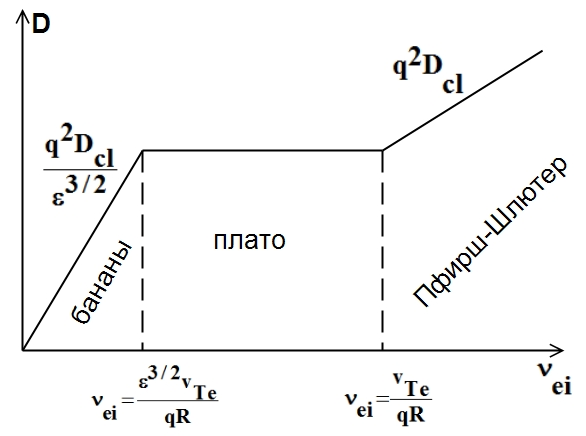
Рис. 12. Зависимость неоклассического коэффициента диффузии

от частоты столкновений

В реальном токамаке коэффициенты диффузии и теплопроводности для ионов могут всего лишь в несколько раз превосходить неоклассические. Для электронов же эти величины могу отличаться на один–два порядка.

В настоящее время не существует общепризнанной теории аномального переноса в токамаке. Поэтому для расчётов используют как численные расчёты на основе гирокинетического уравнения, в котором произведено усреднение обычного кинетического уравнения по ларморовскому вращению, так и различные эмпирические модели.

Для оценки глобального энергетического времени удержания тепла 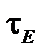применяют так называемые скейлинги. Хорошей эмпирической формулой для токамаков с невысокой плотностью плазмы является скейлинг Мережкина–Муховатова (скейлинг Т-11):

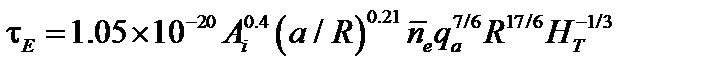. (5.2.21)

Здесь 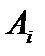– атомный номер рабочего газа (для дейтерия 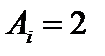), , 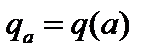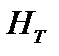– тороидально магнитное поле. Время измеряется в секундах, радиусы – в сантиметрах, плотность – в см^-3, магнитное поле – в гауссах. Этот результат близок к теоретической формуле Кадомцева–Погуце для электронной теплопроводности:

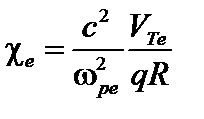(5.2.22)

или близкой к ней формуле Окавы, которая не содержит фактора 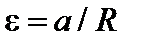. Основное отличие состоит в том, что формула (5.2.21) содержит множителя 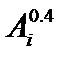, то есть не включает так называемого «изотоп-эффекта», наблюдаемого экспериментально. Заметим, что неоклассические коэффициенты переноса даже растут с увеличением атомного номера рабочего газа, что противоречит эксперименту. Теоретические модели, основанные на нелинейном рассмотрении баллонных мод, то есть мод, связанных с «выпячиванием» магнитных поверхностей, аналогичном выпячиванию наружу надуваемой велосипедной камеры, дают правильную зависимость коэффициентов переноса от атомного номера рабочего газа ([4, 6]).

Эмпирические скейлинги для ИТЭР учитывают значительное увеличение времени удержания, когда мощность нагрева превосходит некоторую критическую величину, так называемый L-H (low-high) переход. Для L-режима скейлинг ИТЭР выглядит так:

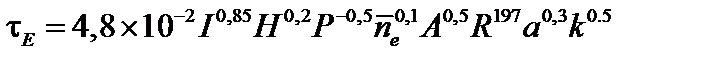. (5.2.23)

При более высокой мощности нагрева реализуется -режим. Для H -режима скейлинг имеет следующий вид:

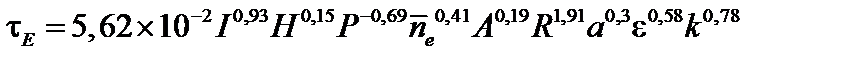. (5.2.24)

Здесь 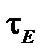измеряется в секундах, ток I – в MA, магнитное поле H – в Tл, полная вводимая в плазму мощность Р – в МГДж, R и a – в метрах, 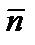– в м^-3 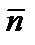– средняя по объему плотность в м^-3. Величина 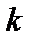характеризует вытянутость сечения токамака в вертикальном направлении.