В этом разделе мы рассмотрим классические, то есть не учитывающие тороидальных эффектов и турбулентности переносы в плазме. Уравнение непрерывности, описывающее переносы в направлении, перпендикулярном магнитным поверхностям, имеет вид
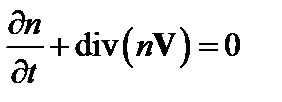 . (5.1.1)
. (5.1.1)
Пока мы не конкретизировали вида перпендикулярной скорости отдельной частицы, такое уравнение описывает как классические переносы, так и аномальные. Будь то длина пробега в незамагниченной плазме, или ларморовский радиус в замагниченной, или расстояние, на которое частица переносится благодаря однократному взаимодействию с волной, если эта величина много меньше характерного размера задачи, например малого радиуса плазмы в токамаке, то такой перенос носит диффузионный характер. Поток плазмы, перпендикулярный магнитному полю, 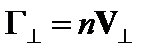 , пропорционален коэффициенту диффузии
, пропорционален коэффициенту диффузии 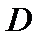 . В одномерном случае в отсутствие источников можно написать
. В одномерном случае в отсутствие источников можно написать
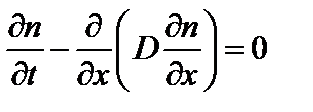 . (5.1.2)
. (5.1.2)
По порядку величины запишем
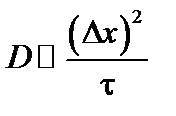 , (5.1.3)
, (5.1.3)
где 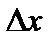 – длина пробега между столкновениями, а
– длина пробега между столкновениями, а 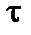 – время между ними. В спокойной замагниченной плазме для частиц сорта
– время между ними. В спокойной замагниченной плазме для частиц сорта 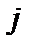 роль
роль 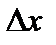 играет ларморовский радиус
играет ларморовский радиус 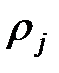 , а роль
, а роль 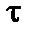 – обратная частота кулоновских столкновений
– обратная частота кулоновских столкновений 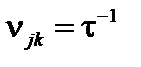 частиц сорта
частиц сорта 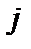 с частицами сорта
с частицами сорта 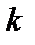 , и по порядку величины имеем
, и по порядку величины имеем
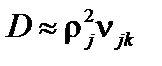 . (5.1.4)
. (5.1.4)
Классический коэффициент диффузии можно более точно выразить через частоту столкновений. Для этого рассмотрим стационарное уравнение импульса для частиц сорта 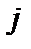 , сталкивающихся с частицами сорта
, сталкивающихся с частицами сорта 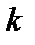 :
:
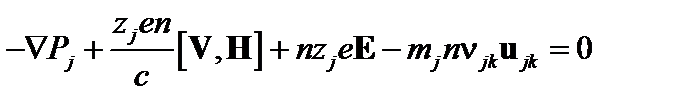 . (5.1.5)
. (5.1.5)
Здесь 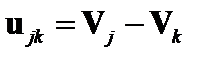 . Умножая это уравнение на
. Умножая это уравнение на  векторно и раскрывая двойное векторное произведение, получаем
векторно и раскрывая двойное векторное произведение, получаем
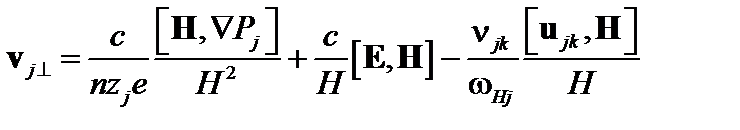 ; (5.1.6)
; (5.1.6)
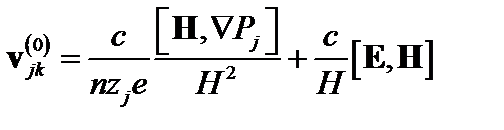 . (5.1.7)
. (5.1.7)
В первом приближении получаем
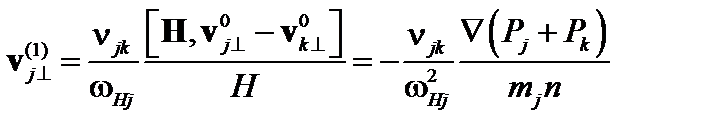 . (5.1.8)
. (5.1.8)
Рассмотрим случай, когда 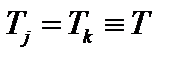
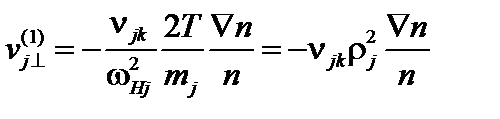 . (5.1.9)
. (5.1.9)
Поток частиц в направлении, перпендикулярном магнитному полю, пропорционален плотности и не зависит от сорта частиц
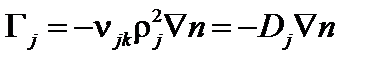 . (5.1.10)
. (5.1.10)
Действительно, из третьего закона Ньютона 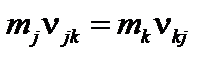 , квадрат ларморовского радиуса пропорционален массе частицы, а коэффициент диффузии
, квадрат ларморовского радиуса пропорционален массе частицы, а коэффициент диффузии 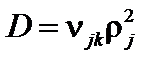 от неё не зависит. Таким образом, классическая диффузия автоматически амбиполярна,
от неё не зависит. Таким образом, классическая диффузия автоматически амбиполярна, 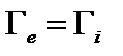 .
.
 2015-08-21
2015-08-21 498
498








