2015-08-21
376
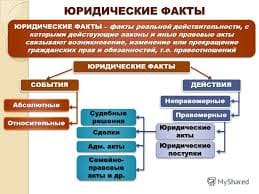
The problem about finding the shortest path length in a connecting network refers to the fundamental combinatory optimization problems. It is possible to reduce a wide range of the practical problems originating in various areas of a national economy, and first of all in communication.
D e f i n i t i o n. The path is the sequence of vertices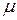 
ir = (i, j, …, r) or sequence of arches (ribs) 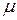ir = {(i, j), … (to, r)}, connecting pair of vertices i and r of graph G.
The sum of the weights attributed to arches (ribs) in path 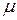ir defines a path length.
The way from an vertex i into an vertex r possessing minimum possible length is called the shortest way.
The network is called connecting if there is at least one way connecting them for each pair of vertices.
Being based on network model, the problem about finding the shortest way can be formulated by the following way.
Let connecting network G be given where every arch (rib) has the positive weight that is proportional to its length. It is required to find a way 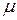st between the set vertices s and t, having minimum possible length, i.e.
L =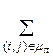 
lijÒ min (on M),
where M – a set of all possible ways from s to t.
One of the most effective algorithms solving the given task is Dijkstra algorithm having the author’s name.
This algorithm feature is the fact that during its performance the shortest ways are simultaneously under construction from the set vertex s into all other network vertices. It can be explained by the fact that any vertex i _ N can appear intermediate in the shortest way from s in t. At the end of algorithm operation the vertex s appears connecting with all other network G vertices as well as with an vertex t, the shortest ways, and the arches (rib) having entered into them, form some sub-network without cycles, i.e. a tree with a root in an vertex s.
Algorithm operation is introduced by means of arrangement at vertices aspect (Lsj, i) marks, where Lsj - length of the shortest way from an initial vertex s into some vertex j, and i preceding j vertex in this path.
Marks are divided into time and constant. Time marks can change as a result of algorithm operation, and the constants – do not change.
Dijkstra algorithm in the step-by-step form is given below.
Step 0. For vertex s Lss = 0 is considered, and for other vertices Lsj =ђ. All vertices have time marks of an aspect (Lsj, s).
Step 1. Among vertices with time marks we choose vertex r, for which Lsr=min (Lsj). The apex mark r becomes constant.
Step 2. If all vertices of a network obtained constant marks it means the end of algorithm operation. Otherwise - transition to a step 3.
Step 3. We enumerate time marks for vertices contiguous to vertex obtained a constant mark on a step 1, according to expression Lsj= min (Lsj, Lsr+Lrj).
Transition to a step 1.
Path trace 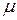st is made in the inverse direction following from an vertex t in s, being guided by vertices i in constant marks.
Let's illustrate the Dijkstra’s algorithm operation on an instance.
Let's find the shortest way from the vertex s to the vertex t in a network represented on fig. 2.9. The weights put down near ribs define their length.
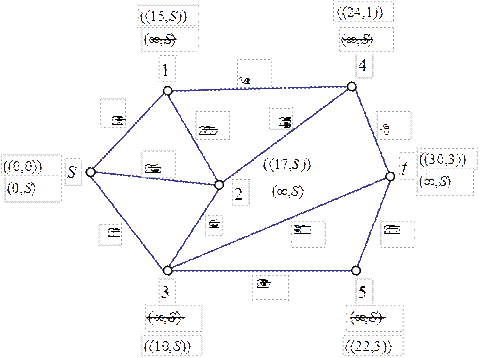
Figure 2.9 – Illustration work of algorithm of Dijkstra
Step 0. Mark P for vertex s looks like: Рs =(0,0). For other vertices Рi = (ђ, s). All marks are time ones.
Step 1. Among time marks the vertex s has the least length parameter as Lss= 0. Its mark becomes a constant one (we will note it with double brackets)
Step 2. We convert time marks for vertices contiguous to vertex s. For the vertex 1 the parameter length
Ls1=Lss+ls1= 0 + 15 = 15
The obtained value is less than available one(Lsi=ђ)and consequently a new value of a time mark will be P 1 = (15, s).
For the vertex 2 a new mark has the value P 2 = (17, s). For the vertex 3 – P 3 = (10, s).
Passing to a step 1, we choose the vertex 3 as it has the least length parameter Ls3= 10, among all vertices with time marks. Its mark becomes a constant one. As not all vertices have obtained constant marks we pass to a step 2 and we carry out the re-count of marks for vertice, contiguous to an vertex 3:
P 2 = (17, s) can de left without changing as the new length parameter is equal to former value.
P 5 = (22, 3).
P t = (30, 3).
The vertex 1 on a step 1 obtains a constant mark as its length parameter is minimum.
New value of a mark on a step 2 is obtained by the vertex 4, namely
P 4 = (24, 1).
Coming back to a step 1, we set a constant mark for
vertex 5. To change the value of marks on a step 3 is impossible. We fix the following vertex with a constant mark it is the vertex 4.
To change a time mark for the vertex t is impossible – and it automatically becomes a constant one.
Here algorithm operation comes to an end.
We define the way trace 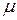st moving in the opposite direction from t to s through the vertices specified in marks: t 
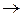3 s.
