Функція f(х,у) отримується з функції g(х,у) за допомогою операції сумування, якщо для всіх х, у є N маємо 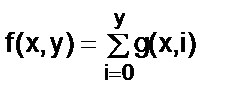 .
.
Функція f(х,у) отримується з функції g(х,у) за допомогою операції мультиплікації, якщо для всіх х, у є N маємо 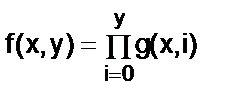 .
.
Функція f(x1,..., xn) елементарнa (елементарнa за Кальмаром), якщо вона може бути отримана з функцій s, I 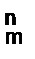 , + та
, + та 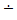 за допомогою скінченної кількості застосувань операцій суперпозиції, сумування і мультиплікації.
за допомогою скінченної кількості застосувань операцій суперпозиції, сумування і мультиплікації.
Наступні співвідношення встановлюють елементарність відомих функцій:
1) о (x) = х 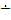 х;
х;
2) 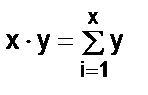 ;
;
3) (х) = s (о (х));
4) 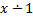 =
= 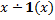
5) sg(x) = x 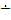 (х
(х 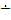 1);
1);
6) nsg(x) = 1 (х) 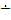 х;
х;
8) mod(х, у) = х 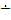 (у
(у 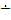 х / у])
х / у])
9)C(x, y)=[((x+y)2 + 3*x+y)/2];
10) x! =x∏i=1 i
11) xy=y∏ i=1 I21(x,i).
Нехай f(х) отримана за допомогою операції кускового завдання з функцій g1(x),..., gn(x) та допоміжних функцій α1(x),..., αn(x): f(х) = g1(x)×nsg(α1(x))+...+gn(x)×nsg(αn(x)).
Тоді f(х) – елементарна функція, якщо функції gi(x), αi(x), де 1£ i £n, елементарні.
Нехай f(х) = μy£α(x)(g(х, у)=0) отримана за допомогою операції обмеженої мінімізації. Тоді функцію f(х) можна задати у вигляді f(х)=h(х,α(x)), де 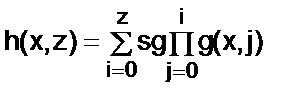 .
.
Звідси f(х) елементарна функція, якщо функції g(х,у) та α(x) елементарні.
Кажуть, що функція f(х,у) отримується за допомогою операції обмеженої рекурсії з функцій g(х), h(х, у, z) та φ(х, у), якщо:
1) функція f(х, у) задається схемою примітивної рекурсії f(х, 0) = g(х), f(х, у) = h(х, у 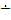 1), f(х, у
1), f(х, у 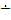 1)),
1)),
2) для всіх х, у є N маємо f(х, у)£φ (х, у).
Теорема. Нехай функція f(х, у) отримана за допомогою операції обмеженої рекурсії з функцій g(х), h(х, у, z) та φ(х, у), причому функції g(х), h(х,у,z) та φ(х,у) – елементарні. Тоді f(х, у) також елементарна.
Визначимо операцію обмеженої рекурсії в загальному випадку. Нагадаємо, що 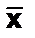 є скороченим позначенням послідовності x1,..., xn
є скороченим позначенням послідовності x1,..., xn
Скажемо, що функція f(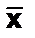 , у) отримана за допомогою операції обмеженої рекурсії з функцій g(
, у) отримана за допомогою операції обмеженої рекурсії з функцій g(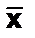 ), h(
), h(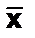 , у, z) та φ(
, у, z) та φ(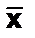 , у), якщо вона задана схемою примітивної рекурсії
, у), якщо вона задана схемою примітивної рекурсії
f(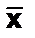 , 0) = g(
, 0) = g(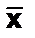 ), f(
), f(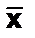 , у) = h(
, у) = h(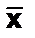 ,у
,у 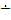 1), f(
1), f(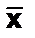 ,у
,у 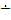 1)),
1)),
причому для всіх 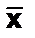 єNn та уєN маємо f(
єNn та уєN маємо f(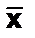 , у) £ φ(
, у) £ φ(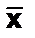 , у).
, у).
Має місце природне узагальнення теореми 9.1.1.
Теорема. Нехай функція f(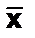 , у) отримана за допомогою операції обмеженої рекурсії з елементарних функцій g(
, у) отримана за допомогою операції обмеженої рекурсії з елементарних функцій g(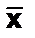 ), h(
), h(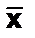 , у, z) та φ(
, у, z) та φ(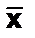 , у). Тоді функція f(
, у). Тоді функція f(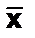 , у) також елементарна.
, у) також елементарна.
 2015-08-21
2015-08-21 379
379








