Нехай 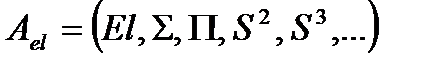 , де носій El – клас елементарних функцій;
, де носій El – клас елементарних функцій; 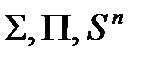 – це операції.
– це операції.
Алфавіт: 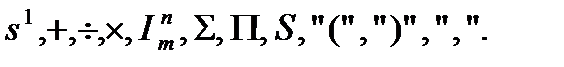
Визначення операторного терму:
1. Усі символи базових функцій є операторними термами.
2. Якщо 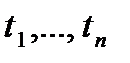 є операторними термами для завдання m-арних функцій, а
є операторними термами для завдання m-арних функцій, а 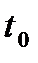 є термом для задання n-арної функції, то терм
є термом для задання n-арної функції, то терм 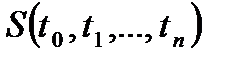 є термом для позначення m-арної функції.
є термом для позначення m-арної функції.
3. Якщо 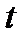 є операторним термом для бінарної функції, то терми
є операторним термом для бінарної функції, то терми 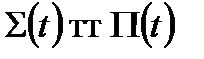 є операторними термами для бінарних функцій.
є операторними термами для бінарних функцій.
4. Інших оператор них термів не існує.
Зрозуміло, що кожна елементарна функція є ПРФ. Доведемо зворотне твердження – що це включення строге.
Для цього розглянемо допоміжну функцію 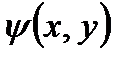 :
: 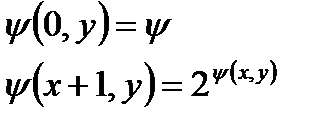
Функцію 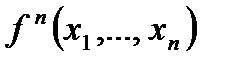 назвемо k -східчастою, якщо має місце умова:
назвемо k -східчастою, якщо має місце умова: 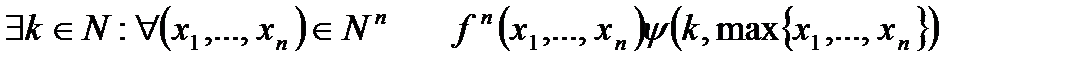 .
.
Теорема: Довільна елементарна функція є k -східчастою для певного відповідного значення k.
Доведення:
· Базові функції:
o 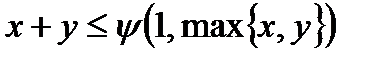
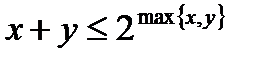
o так само для  ;
;
o 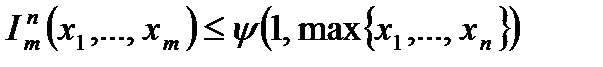 .
.
· Нехай 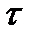 є операторним термом для бінарної функції
є операторним термом для бінарної функції 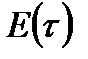 . Утворимо функції
. Утворимо функції 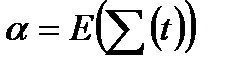 та
та 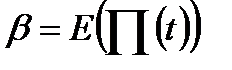 (обидві вони бінарні). Нехай
(обидві вони бінарні). Нехай 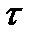 є
є 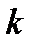 -східчастою функцією. Тоді
-східчастою функцією. Тоді 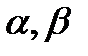 є
є 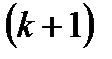 -східчастими функціями.
-східчастими функціями.
o Це випливає з двох нерівностей:
§ 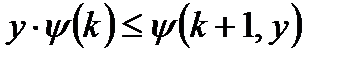
§ 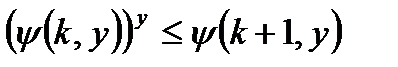
o Обидві вони доводяться математичною індукцією.
· Нехай 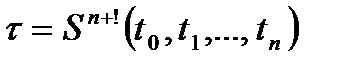 , де
, де 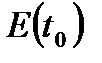 -
- 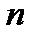 -арна функція, а
-арна функція, а 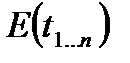 -
- 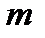 -арні. Тоді
-арні. Тоді 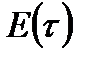 є
є 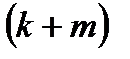 -арною функцією.
-арною функцією.
Покажемо тепер, що існує ПРФ, яка не є елементарною.
Наприклад, візьмемо функцію 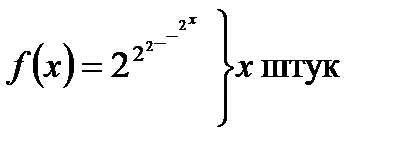 . Для такої функції не існує такого єдиного
. Для такої функції не існує такого єдиного 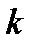 , для якого можна було б мажорувати цю функцію
, для якого можна було б мажорувати цю функцію 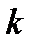 -східчастою.
-східчастою.
 2015-08-21
2015-08-21 309
309








