2015-08-21
4757
Описание алгоритма:
Метод ориентирован на решение задач с квадратичными целевыми функциями. Основная идея алгоритма заключается в том, что если квадратичная функция:
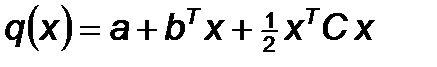
приводится к виду сумма полных квадратов
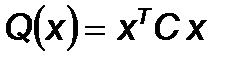
то процедура нахождения оптимального решения сводится к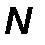 
одномерным поискам по преобразованным координатным направлениям.
В методе Пауэлла поиск реализуется в виде:
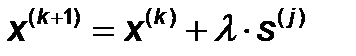
вдоль направлений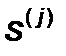 
, 
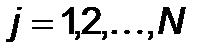, называемых 
-сопряженными при линейной независимости этих направлений.
Сопряженные направления определяются алгоритмически. Для нахождения экстремума квадратичной функции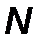 
переменных необходимо выполнить 
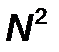одномерных поисков.
Алгоритм метода:
Шаг 1. Задать исходные точки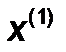 
, 
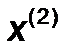и направление 
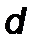. В частности, направление 
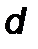может совпадать с направлением координатной оси;
Шаг 2. Произвести одномерный поиск из точки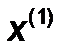 
в направлении 
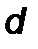получить точку 
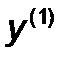, являющуюся точкой экстремума на заданном направлении;
Шаг 3. Произвести одномерный поиск из точки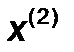 
в направлении 
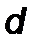получить точку 
;
|
|
|
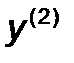Шаг 4. Вычислить направление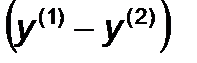 
;
Шаг 5. Провести одномерный поиск из точки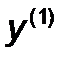 
(либо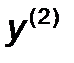 
) в направлении 
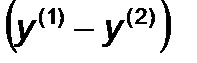с выводом в точку 
.
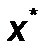Ход решения:
Исходные данные:
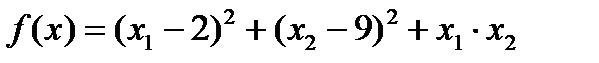
Шаг 1.
Пусть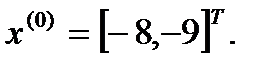 
.
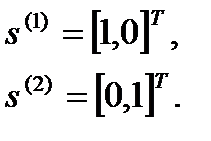
Итерация 1:
Шаг 2.
1) найдём значение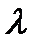 
, при котором 
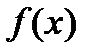минимизируется в направлении 
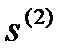, т.е.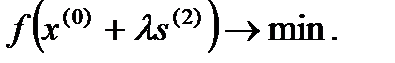 
Произвольная точка на луче из точки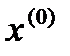 
в направлении 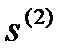определяется как:
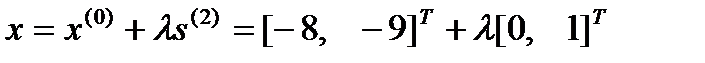, откуда 
, 
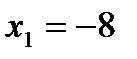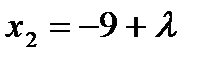. Подставляя эти значения в выражение целевой функции, получаем:
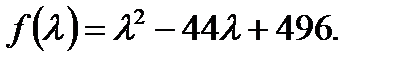
Дифференцируем по 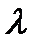и приравниваем к 0, получаем:
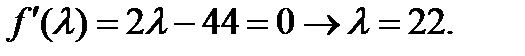
Получаем:
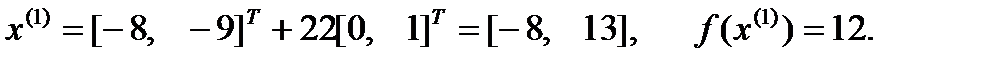
2) Аналогично находим значение 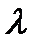, при котором 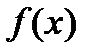минимизируется в направлении 
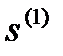, т.е.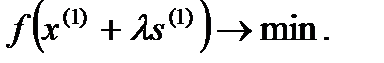 
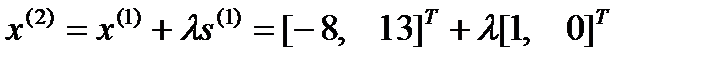, откуда 
, 
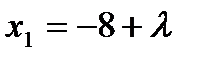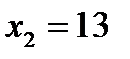. Подставляя эти значения в выражение целевой функции, получаем:
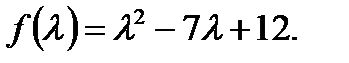
Дифференцируем по 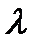и приравниваем к 0, получаем:
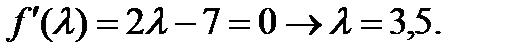
Получаем:
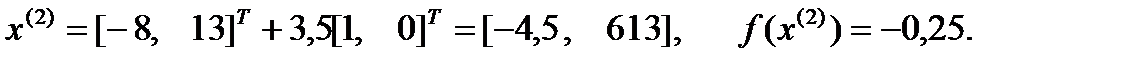
3) Аналогично находим значение 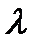, при котором 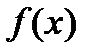минимизируется в направлении 
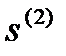, т.е.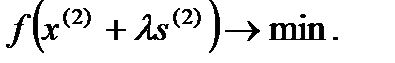 
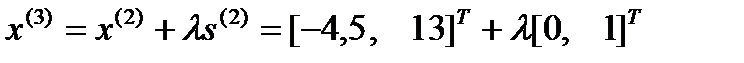, откуда 
, 
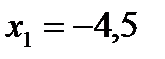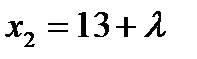. Подставляя эти значения в выражение целевой функции, получаем:
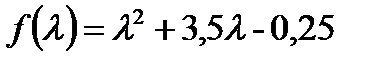
Дифференцируем по 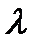и приравниваем к 0, получаем:
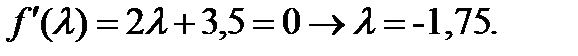
Получаем:
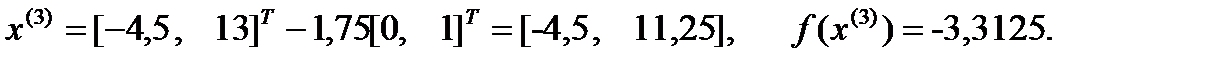
Шаг 3.
Положим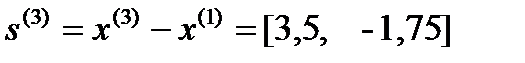 
.
Направление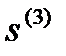 
оказывается сопряжённым с направлением 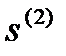. Оптимизация вдоль направления 
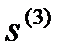даёт искомый экстремум.
Шаг4.
Находим значение 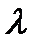, при котором 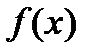минимизируется в направлении 
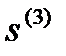, т.е.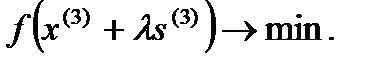 
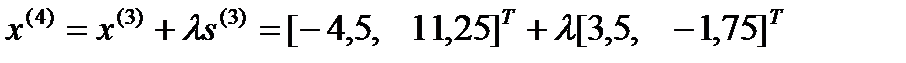, откуда 
, 
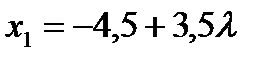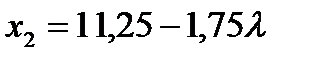. Подставляя эти значения в выражение целевой функции, получаем:
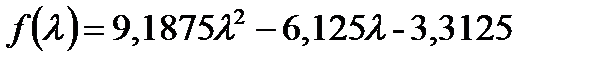
Дифференцируем по 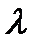и приравниваем к 0, получаем:
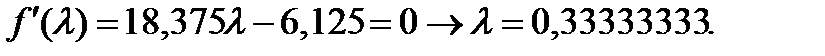
Получаем:
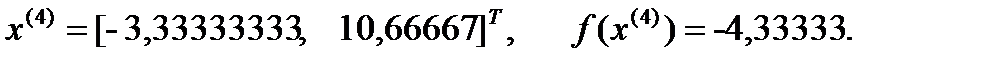
Итерация 2:
Шаг 2.
1) найдём значение 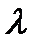, при котором 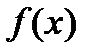минимизируется в направлении 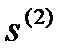, т.е.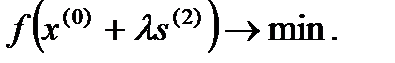
Произвольная точка на луче из точки 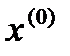в направлении 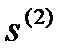определяется как:
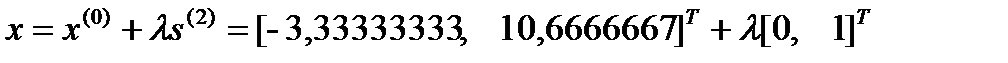, откуда 
, 
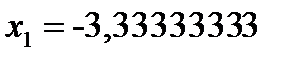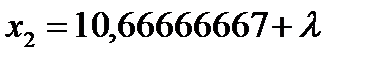. Подставляя эти значения в выражение целевой функции, получаем:
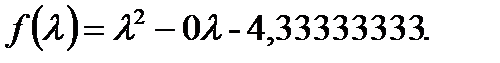
Дифференцируем по 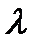и приравниваем к 0, получаем:
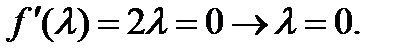
Получаем:
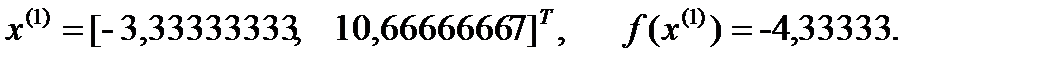
2) Аналогично находим значение 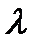, при котором 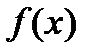минимизируется в направлении 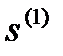, т.е.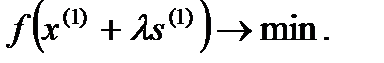
|
|
|
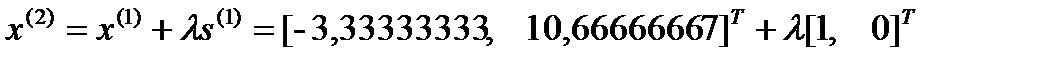, откуда 
, 
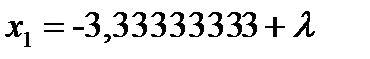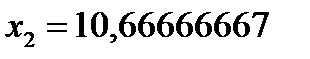. Подставляя эти значения в выражение целевой функции, получаем:
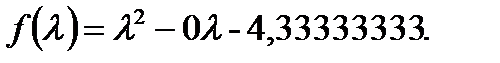
Дифференцируем по 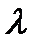и приравниваем к 0, получаем:
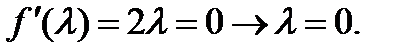
Получаем:
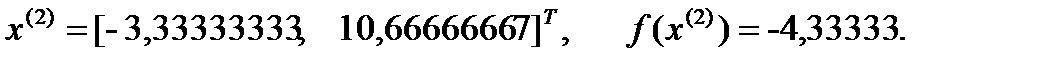
3)Аналогично находим значение 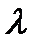, при котором 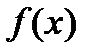минимизируется в направлении 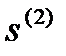, т.е.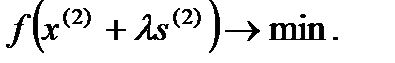
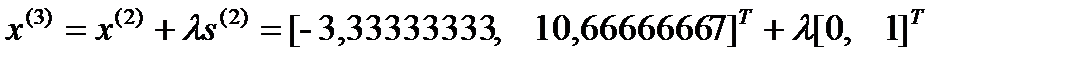, откуда 
, 
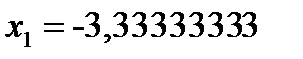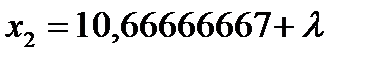. Подставляя эти значения в выражение целевой функции, получаем:
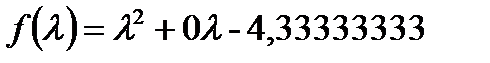
Дифференцируем по 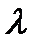и приравниваем к 0, получаем:
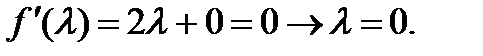
Получаем:
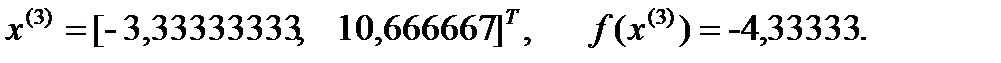
Шаг 3.
Положим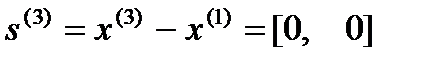 
.
Направление 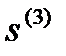оказывается сопряжённым с направлением 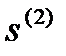. Оптимизация вдоль направления 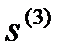даёт искомый экстремум.
Шаг 4.
Находим значение 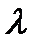, при котором 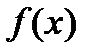минимизируется в направлении 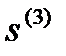, т.е.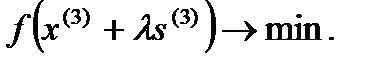
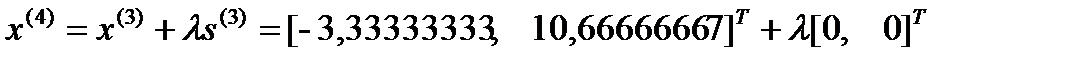, откуда 
, 
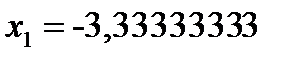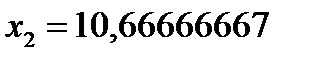. Подставляя эти значения в выражение целевой функции, получаем:
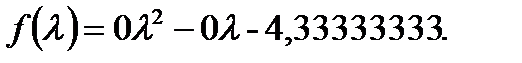
Дифференцируем по 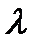и приравниваем к 0, получаем:
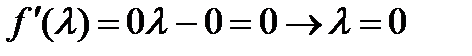
Получаем:
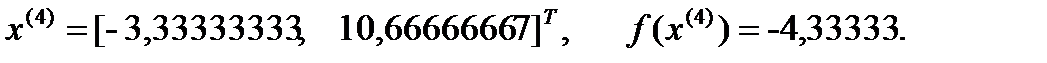
Решение поставленной задачи методом сопряжённых направлений Пауэлла представлено на рисунке 3.
|
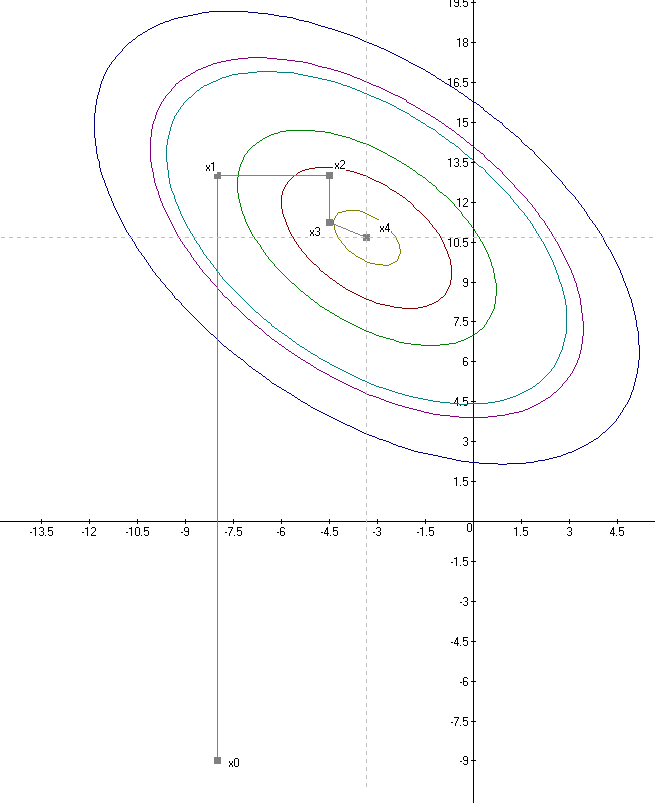| Рисунок 3 – решение задачи методом сопряжённых направлений Пауэлла |
