Описание алгоритма:
Данный метод обладает положительными свойствами методов Коши и Ньютона. Кроме того, этот метод использует информацию только о первых производных исследуемой функции. Метод сопряженных градиентов позволяет получить решение за 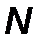 шагов в
шагов в 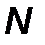 -мерном пространстве и обладает квадратичной сходимостью. В основе метода лежит организация поиска вдоль сопряженных направлений, причем для получения сопряженных направлений используется квадратичная аппроксимация целевой функции и значения компонент градиента.
-мерном пространстве и обладает квадратичной сходимостью. В основе метода лежит организация поиска вдоль сопряженных направлений, причем для получения сопряженных направлений используется квадратичная аппроксимация целевой функции и значения компонент градиента.
Операции аргумента проводятся по формуле:
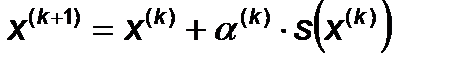
Направление поиска на каждой итерации определяется с помощью формулы:
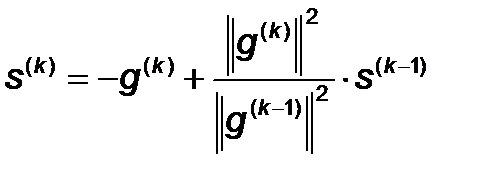
В этом случае направление 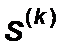 будет
будет  -сопряжено со всеми ранее построенными направлениями поиска.
-сопряжено со всеми ранее построенными направлениями поиска.
Если функция 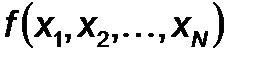 квадратичная, то для нахождения точки экстремума требуется определить
квадратичная, то для нахождения точки экстремума требуется определить 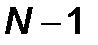 таких направлений и провести поиски вдоль каждой прямой. Если
таких направлений и провести поиски вдоль каждой прямой. Если 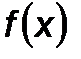 не является квадратичной, то количество поисков возрастёт.
не является квадратичной, то количество поисков возрастёт.
Используемые в методе формулы:
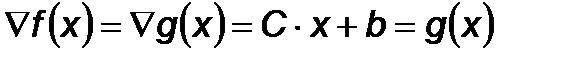
Изменение градиента при переходе от точки 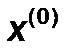 к точке
к точке 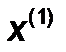 :
:
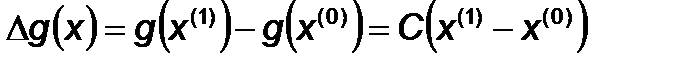
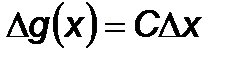
Изменения аргумента:
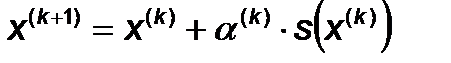
Направление поиска:
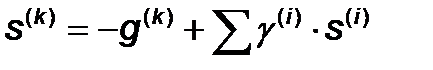 ,
, 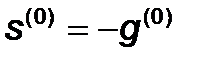 ,
, 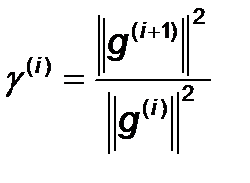 .
.
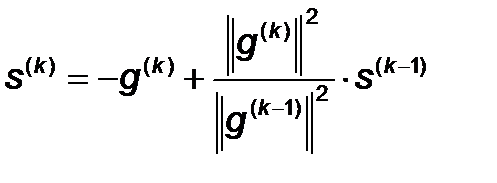 (рекуррентная формула Флетчера-Ривса).
(рекуррентная формула Флетчера-Ривса).
Алгоритм метода:
Шаг 1. Задать: начальную точку х(0). Перейти к шагу 2.
Шаг 2. Вычислить направление поиска. Произвести поиск вдоль прямой 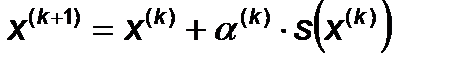 .
.
Шаг 3. Вычислено ли N-1 направлений.
Да: закончить поиск;
Нет: перейти к шагу 2.
Ход решения:
Исходные данные:
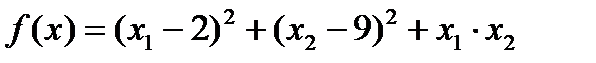
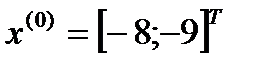
Шаг 1:
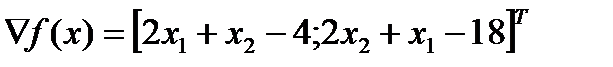 .
.
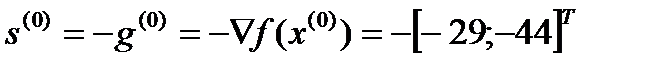 .
.
 2015-08-21
2015-08-21 991
991








