2015-08-21
238
Рассмотрим каноническую задачу ЛП:
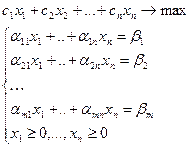
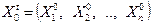
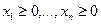
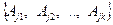Решение системы линейных уравнений из системы ограничений задачи Lk называется базисным, если система векторов, соответствующих ненулевым значениям неизвестных в X 0, является линейной независимой. При этом, если все координаты X 0 неотрицательны, то такое решение называется опорным.
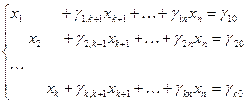Пусть система ограничений задачи ЛП Lk приведена к единичному базису и без ограничения общности имеет следующий вид:
(1)
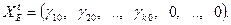Здесь x 1, …, xk – базисные неизвестные, xk+ 1, …, xn – свободные неизвестные.
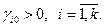Соответственное базисное решение равно
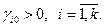Это базисное решение будет опорным тогда и только тогда, когда все
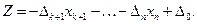Опорный план называется невырожденным, если все
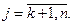Выразим целевую функцию z (x) через свободные неизвестные:
Число D j при свободной неизвестной xj называется оценкой этой неизвестной
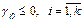
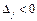
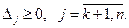Критерий оптимальности. Опорное решение, соответствующее системе ограничений, является оптимальным, если все оценки свободных неизвестных неотрицательны:
Критерий неразрешимости. Если существует оценка, такая что в системе (1), то задача Lk неразрешима из-за неограниченности целевой функции.
|
|
|
Запишем задачу Lk в виде следующей таблицы, предполагается, что x 1, …, xk – базисные неизвестные.
| С | Б | x 1 | x 2 | … | xk | xk +1 | … | xn | H |
| c 1 | c 2 | ck | ck +1 | cn | |||||
| c 1 | x 1 | g1, k +1 | g1 n | g10 | |||||
| c 2 | x 2 | g2, k +1 | g2 n | g20 | |||||
| … | … | … | … | … | … | … | |||
| ck | xk | g k , k +1 | g kn | g k 0 | |||||
| Z | … | D k +1 | … | D n | D0 |
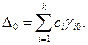
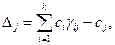В первом столбце С расположены коэффициенты при базисных неизвестных в целевой функции, во втором столбце Б – базисные неизвестные, следующие столбцы задают систему ограничений (1).
Оценка D j неизвестной xj находится по формуле:
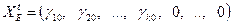Этой таблице соответствует базисное решение:
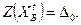Значение целевой функции
