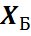
| 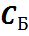
| 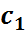
| 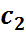
| … | 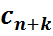
| 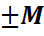
| … | 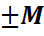
| В |
| 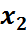
| … | 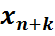
| 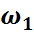
| … | 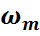
| |||
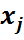
| 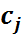
| 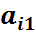
| 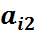
| … | … | … | … | … | |
| … | … | … | … | … | … | … | … | …. | … |

| 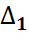
| 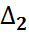
| … | … | … | … | … | 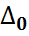
|
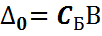 ,
, 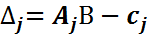 – индексные оценки.
– индексные оценки.
Пример.
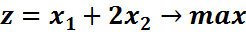
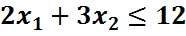
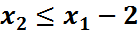
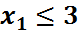
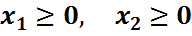
Перепишем второе неравенство так, чтобы свободный член был положительным:
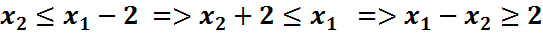
Получим систему ограничений:
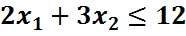
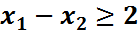
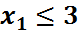
Превратим неравенства в равенства, для чего введем дополнительные переменные.
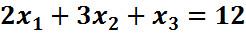
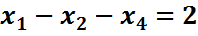
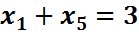
В целевую функцию эти переменные войдут с нулевыми коэффициентами.
Выделим базисные переменные, т.е. такие, которые входят только в одно уравнение с коэффициентом (+1) и не входят в другие уравнения.
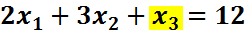
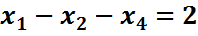
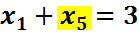
Во втором уравнении такой переменной нет, поэтому добавим искусственную базисную переменную 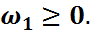 в целевую функцию эта переменная войдет с коэффициентом (-М), т.к. решается задача на максимум. Получим М – задачу:
в целевую функцию эта переменная войдет с коэффициентом (-М), т.к. решается задача на максимум. Получим М – задачу:
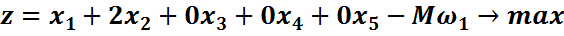
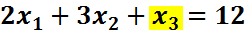
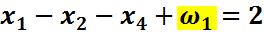
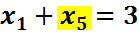
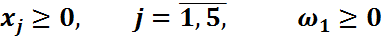
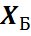
| 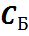
| -M | В | |||||
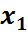
| 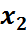
| 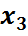
| 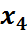
| 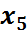
| 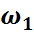
| |||
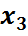
| ||||||||
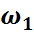
| -M | -1 | -1 | |||||
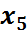
| ||||||||

| -M | M | M | -2M | ||||
| -1 | -2 |
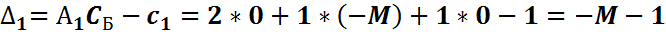
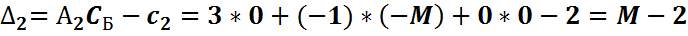
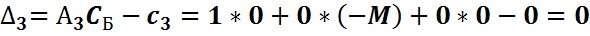
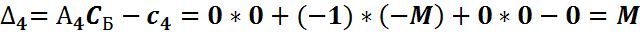
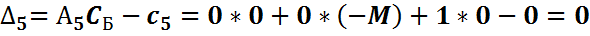
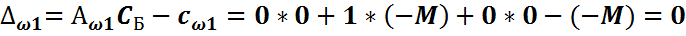
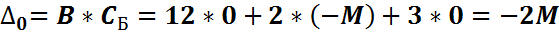
 2015-08-21
2015-08-21 229
229








