2015-08-21
423
РЕШЕНИЕ ЗЛП СИМПЛЕКС МЕТОДОМ
ЗЛП нужно привести к канонической форме
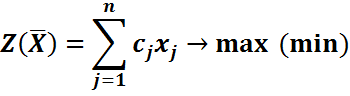
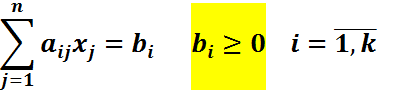
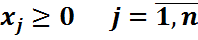
Для этого
А)во всех ограничениях
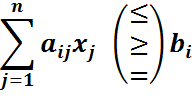
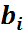делают неотрицательными. Т.е., если нужно, умножают всю строку на (-1).
В)превращают неравенства в равенства, для чего вводят дополнительные переменные.
Если имелось неравенство
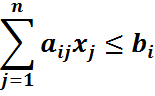
то к левой части прибавляют неотрицательную переменную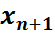 
и получают уравнение
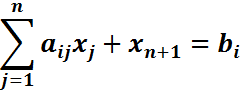
В целевую функцию эта переменная войдет с нулевым коэффициентом.
Если имелось неравенство
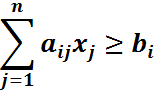
то из левой части вычитают неотрицательную переменную 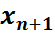и получают уравнение
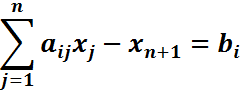
В целевую функцию эта переменная войдет с нулевым коэффициентом.
2)Выделяют базисные переменные, т.е. такие, которые входят только в одно уравнение с коэффициентом (+1) и не входят в другие уравнения. Если в уравнении такой переменной нет, то добавляют искусственную базисную переменную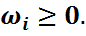 
В целевую функцию эта переменная войдет с коэффициентом +М, если решается задача на минимум, и с коэффициентом (-М), если решается задача на максимум. Здесь М – большое положительное число. Получают М – задачу.
