Моделювання нормально-розподілених випадкових величин

Нехай потрібно отримати послідовність випадкових чисел, що мають нормальний розподіл

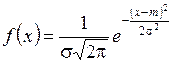, (2.22)

де m,σ – математичне сподівання та середньоарифметичне відхилення.

Надалі випадкові величини, розподілені за нормальним законом, будемо позначати х Î N(m, σ ). Для моделювання такої випадкової величини не можна безпосередньо скористатися методом оберненої функції, оскільки неможливо аналітично розв’язати рівняння (2.16), бо інтеграл 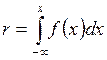не можна виразити через елементарні функції. Тому для моделювання слід скористатися методом кусково-лінійної апроксимації або методом згорток.

Застосування методу кусково-лінійної апроксимації передбачає отримання випадкових величин х Î N (m, σ) у два етапи. На першому етапі здійснюється методом кусково-лінійної апроксимації генерування нормованої нормально-розподіленої випадкової величини х_n (m_xn= 0 і σ_xn= 1).

На другому етапі визначаємо Х за допомогою перетворення

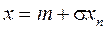. (2.23)

Щоб одержати на першому етапі х_n Î N (0, 1) побудуємо кусково-лінійну апроксимацію функції розподілу

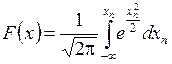. (2.24)

Тобто, представимо (2.24) у табульованому вигляді (F_i, x_н). Для цього розіб’ємо ординату функції F (x_n) на n ділянок.

Використовуючи методи чисельного інтегрування, визначаємо таку величину x_ni, для якої права частина рівняння (2.24) дорівнюватиме F_i. Використавши цю процедуру для всіх F_i, отримаємо кусково-лінійну апроксимацію (2.24). Тепер можемо використати метод оберненої функції. Якщо r_i потрапляє в інтервал (F_i, F_i-1), то х_n обчислюємо як лінійну інтерполяцію між значеннями оберненої функції у точках 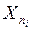і .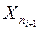

На другому етапі обчислюємо значення 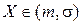за формулою (2.23).

Розглянемо застосування методу згорток [4, 12] для моделювання нормально-розподілених випадкових величин. Цей метод базується на центральній граничній теоремі, яка формується таким чином.

Якщо Х₁, ..., Х_n – послідовність незалежних випадкових величин із мате­матичним сподіванням 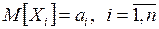і дисперсією 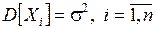, то у разі необмеженого збільшення значення n функція розподілу випадкової величини

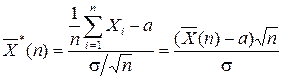
наближається до функції розподілу стандартного нормального закону Ф(z) для усіх значень аргументу, тобто

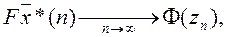
де , .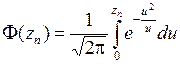

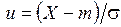Функція Ф (z) називається функцією Лапласа, для значень якої є детальні таблиці.

Алгоритм отримання значень випадкових величин 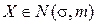передбачає виконання таких кроків. Спочатку генеруємо послідовність випадкових величин 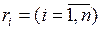, рівномірно розподілених в інтервалі (0,1). Визначаємо суму 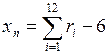. Величина n = 12 є достатнім наближенням до нормально-розподіленої стандартної випадкової величини. Нормальний розподіл з параметрами 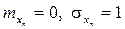називається стандартним. Перехід від випадкової величини X_н Î N (0,1)до випадкової величини X Î N (m, s) здійснюється за допомогою перетворення (2.23).