Моделювання неперервних випадкових величин

Для моделювання значень неперервних випадкових величин повинні бути задані функція розподілу або щільність ймовірності. Серед існуючих методів моделювання неперервних випадкових величин з довільним законом розподі­лу на основі випадкових чисел з рівномірним розподілом в інтервалі (0, 1) розглянемо методи оберненої функції і кусково-лінійної апроксимації. Також моделювання неперервних випадкових величин може бути здійснено на основі граничних теорем теорій ймовірностей, методів відсіювання тощо.

Метод оберненої функції. Розглянемо випадкову величину Х, яка має функцію щільності f(x) і монотонно зростаючу функцію розподілу F(x)

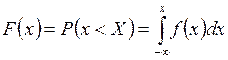. (2.14)

Суть методу полягає у тому, що значення випадкової величини х_і з функцією розподілу F(x) можемо отримати з рівняння F(x_і) = r_і, де r_і – випадкові числа, рівномірно розподілені в інтервалі (0,1). Тоді значення x_і випадкової величини отримується як розв’язок рівняння

X = F ^{- 1} (r), (2.15)

де F ^{- 1} – обернена функція у відношенні до F.

Геометрична інтерпретація методу показана на рис. 2.5.

Таким чином, щоразу, коли необхідно отримати визначене значення випадкових величин х₁, х₂, …, х_n із заданою функцією щільності розподілу f(x) то генеруємо випадкове число r_i Î (0,1) та обчислюємо значення, яке є розв’язком рівняння

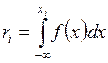. (2.16)

Рис. 2.5. Ілюстрація методу оберненої функції

Розглянемо приклади застосування методу оберненої функції. Змоделюємо неперервну випадкову величину, розподілену за експоненціальним законом. Такий закон набув широкого використання у теорії надійності систем.

Його функція щільності має вигляд

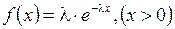. (2.17)

Згідно методу оберненої функції отримаємо

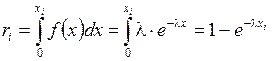
Звідси знаходимо

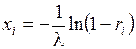(2.18)

Можна показати, що випадкові величини (1 -r_i) та r_i мають один і той же розподіл. Тоді у (2.18) можемо знайти (1 -r_i) на r_i. Отримуємо

.

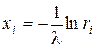Використаємо даний метод для моделювання рівномірно розподіленої в інтервалі [ a, b ] випадкової величини. У цьому випадку щільність і функція розподілу ймовірностей має вигляд (рис. 2.6).

а) б)

Рис. 2.6. Функції щільності (а) і розподілу (б) рівномірно-розподіленої
випадкової величини

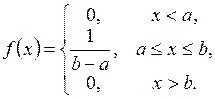
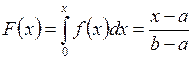. (2.19)

Згідно методу оберненої функції з (2.16) знаходимо

.

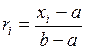Звідси виражаємо значення випадкової рівномірно розподіленої на відрізку [ a, b ] випадкової величини

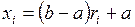. (2.20)

Моделювання неперервних випадкових величин з іншими законами розподілу детально розглянуті у підручнику [12].

Метод кусково-лінійної апроксимації. Цей метод є досить універсальним наближеним способом для моделювання випадкової величини. Суть методу полягає у кусково-лінійній апроксимації функцій розподілу. Він є зручним для алгоритмізації та у багатьох випадках забезпечує необхідну точність перетворення випадкових чисел.

Нехай потрібно привести моделювання неперервної випадкової величини Х із заданим розподілом F (x). Розіб’ємо ординату функцій на n ділянок і відкладемо відповідні значення аргументу на осі абсцис (рис. 2.7).

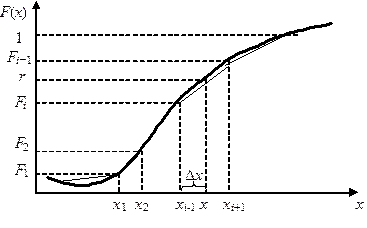
Рис. 2.7. Ілюстрація методу кусково-лінійної апроксимації.

Значення F (x) знаходимо шляхом розв’язання рівняння (2.9). Якщо оберненої функції не існує, то використовуючи метод чисельного інтегрування, отримаємо

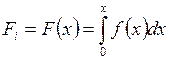
кусково-лінійну апроксимацію функції F(x). Тепер скористаємось методом оберненої функції для кожного інтервалу. Для цього згенеруємо випадкові числа r_iÎ (0,1). Якщо значення r потрапило до і -го інтервалу, то випадкову величину х можна представити у вигляді

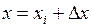, (2.21)

де ∆ х – величина, яка визначається з подібності трикутників (рис. 2.7),

.

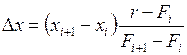Для спрощення інтервад розбивають так, щоб ймовірність попадання випадкової величини у будь-який інтервал (x_k-1, x_k) була сталою.

Таким чином, алгоритм моделювання неперервних випадкових величин методом кусково-лінійної апроксимації зводиться до послідовного виконання таких кроків:

· генеруються r_i Î(0,1);

· за значенням цього числа визначається інтервал (F_i, F_i+1);

· визначається значення випадкової величини за формулою (2.21).