Оценка для хj равна сумме произведений элементов данного столбца на соответствующие элементы первого столбца (Сj-базисные) минус Сj данного столбца (коэффициент над хj).
Например, в первой части таблицы оценка при х2 равна:
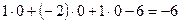 ,
,
в третьей части таблицы оценка при х3 равна:
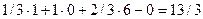 .
.
Значение целевой функции при данном базисе подсчитывается по правилу нахождения оценок. Так, в третьей части таблицы
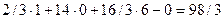 .
.
При решении задачи на максимум опорный план будет оптимальным, если все оценки будут неотрицательными. Исходный опорный план 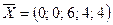 не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
не будет оптимальным, т.к. оценки при х1 и х2 – отрицательные.
По наименьшей отрицательной оценке выбираем разрешающий столбец (столбец х2). Можно перейти к лучшему опорному плану методом однократного замещения, если в этом столбце есть хотя бы один положительный элемент. В нашем примере это условие выполняется. Теперь необходимо выбрать разрешающую строку.
Разрешающую строку определяем по наименьшему θ, равному отношению свободных членов (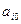 ) к соответствующим положительным элементам разрешающего столбца. В разрешающем столбце х2 два положительных элемента. Находим отношения:
) к соответствующим положительным элементам разрешающего столбца. В разрешающем столбце х2 два положительных элемента. Находим отношения:
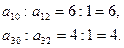
Наименьшим отношением является отношение 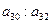 , следовательно,
, следовательно, 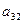 =1 – разрешающий элемент. Неизвестное х2 входит в базис вместо х5. Т.о. посредством преобразования однократного замещения мы перешли к лучшему опорному плану
=1 – разрешающий элемент. Неизвестное х2 входит в базис вместо х5. Т.о. посредством преобразования однократного замещения мы перешли к лучшему опорному плану 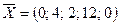 , при котором
, при котором 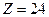 . Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных оценок):
. Но этот план также не является оптимальным, т.к. при х3 оценка отрицательная. В третьей части таблицы получен оптимальный план (нет отрицательных оценок): 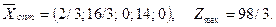
Замечание 1. Оценки и значение целевой функции, начиная со второй части таблицы, следует для контроля считать и по правилу нахождения оценок, и по правилу прямоугольника.
Замечание 2. Если в столбце с отрицательной оценкой нет положительных элементов, то задача оптимального решения не имеет, а целевая функция на множестве допустимых решений неограниченна (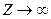 ).
).
Замечание 3. Если требуется найти минимум функции
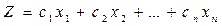 ,
,
то можно перейти к задаче максимизации функции
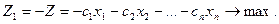
Замечание 4. Признаком альтернативного оптимума задачи является наличие нулевой оценки при свободном неизвестном оптимальной таблицы. В задаче с альтернативным оптимумом необходимо найти
опорные оптимальные планы 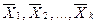 и записать оптимальное решение в виде выпуклой линейной комбинации этих планов:
и записать оптимальное решение в виде выпуклой линейной комбинации этих планов:
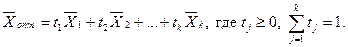
 2015-08-21
2015-08-21 255
255







