Если система ограничений основной задачи каноническая, то задачу линейного программирования можно решить симплексным методом.
Пример 1. Решим задачу симплекс-методом:
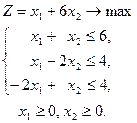
Преобразуем стандартную задачу в основную, добавляя к левым частям ограничений балансовые переменные. Целевая функция при этом не изменится.
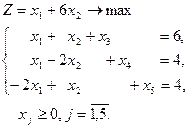
Получим каноническую задачу. Неизвестные 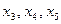 – базисные,
– базисные, 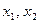 – свободные. Можно записать исходное опорное решение:
– свободные. Можно записать исходное опорное решение: 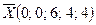 .
.
Составим симплексную таблицу:
| Cj базиса | Базис | C1=1 | C2=6 | C3=0 | C4=0 | C5=0 | θ | |
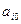
| 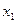
| 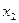
| 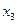
| 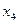
| 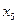
| |||
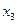
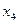
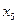
| -2 |
-2
 1 1
| - | |||||
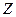 = =
| -1 | -6 | ||||||
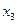
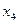
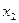
|  3
-3
-2 3
-3
-2
| -1 | 2/3 - - | |||||
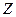 = =
| -13 | |||||||
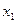
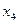
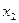
| 2/3 16/3 | 1/3 2/3 | -1/3 1/3 | |||||
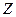 = =
| 98/3 | 13/3 | 5/3 |
Cj – коэффициенты целевой функции. При х1 коэффициент C1=1, при х2 – C2=6, неизвестные х3, х4, х5 отсутствуют в целевой функции, следовательно их коэффициенты равны нулю. В первом столбце таблицы записываются коэффициенты целевой функции, соответствующие базисным неизвестным второго столбца таблицы.
 2015-08-21
2015-08-21 294
294







