Найти максимуму функции 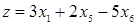 при ограничениях
при ограничениях 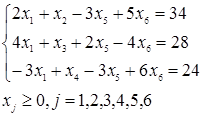 Решим задачу симплекс-методом.
Решим задачу симплекс-методом.
Решение: Перепишем условие задачи в векторной форме: 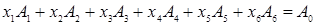 , где
, где 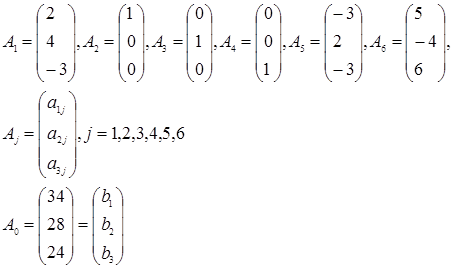 .
.
Среди векторов 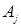 векторы
векторы 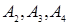 единичные. Примем их за базисные.
единичные. Примем их за базисные.
Составим симплексную таблицу 1.
z= 3x1+ 0x2+ 0x3+ 0x4+ 2x5+ (-5)x6
| i | Базис 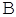
| 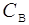
| 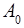
| -5 | |||||
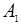
| 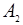
| 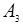
| 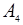
| 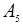
| 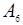
| ||||
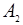
| -3 | ||||||||
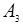
| -4 | ||||||||
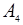
| -3 | -3 | |||||||
m+1 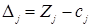
| -3 | -2 |
Найдем разрешающий элемент в таблице 1.
Поскольку 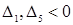 , то найдем
, то найдем 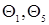 по следующим формулам:
по следующим формулам:
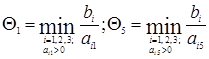 .
.
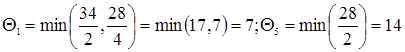 . Таким образом, разрешающий будем выбирать из элементов
. Таким образом, разрешающий будем выбирать из элементов 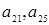 . Для этого найдем минимум из произведений
. Для этого найдем минимум из произведений 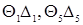 :
:
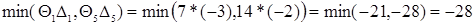 . Тогда разрешающим будет элемент
. Тогда разрешающим будет элемент 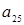 . Следовательно, вместо базисного вектора
. Следовательно, вместо базисного вектора 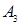 в таблице 1 базисным становится вектор
в таблице 1 базисным становится вектор 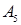 в таблице 2.
в таблице 2.
| i | Базис 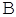
| 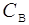
| 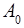
| -5 | |||||
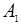
| 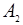
| 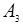
| 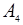
| 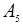
| 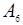
| ||||
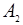
| -3 | ||||||||
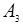
| 2= a25 | -4 | |||||||
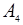
| -3 | -3 | |||||||
m+1 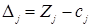
| -3 | -2 |
Построим симплексную таблицу 2, опираясь на разрешающий элемент и следующие правила:
Правило 1: Все элементы k-ой строки (строки в которой находится разрешающий элемент 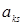 ), начиная со столбца
), начиная со столбца 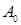 , делятся на разрешающий элемент
, делятся на разрешающий элемент 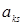 ;
;
Правило 2: Все элементы столбца 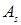 заменяются нулями, кроме
заменяются нулями, кроме 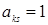 ;
;
Правило 3: Любой элемент 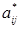 таблицы 2 вычисляется по правилу прямоугольника:
таблицы 2 вычисляется по правилу прямоугольника:
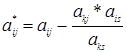
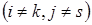 ;
;
Правило 4: (m+1)-строка вычисляется аналогично: 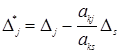 .
.
В таблице 2 базисными будут векторы 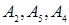 .
.
Таблицу 2.
| i | Базис 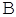
| 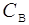
| 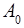
| -5 | |||||
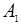
| 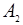
| 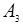
| 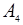
| 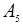
| 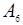
| ||||
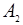
| 3/2 | -1 | |||||||
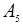
| 1/2 | -2 | |||||||
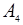
| |||||||||
m+1 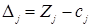
|
Вычислим элементы в столбце 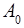 : Вычислим элементы в столбце
: Вычислим элементы в столбце 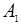 :
:
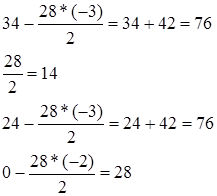
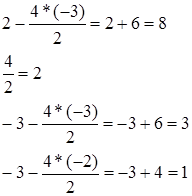
Вычислим элементы в столбце 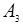 : Вычислим элементы в столбце
: Вычислим элементы в столбце 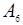 :
:
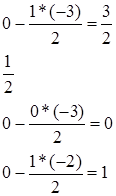
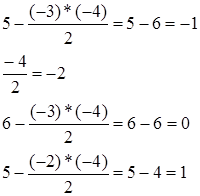
Опорный план найден, так как в (m+1)-строке среди 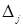 нет отрицательных.
нет отрицательных.
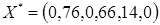 ,
, 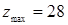 .
.
Замечание 1. После конечного числа шагов получим оптимальный план или докажем отсутствие такового. Оптимальный план отсутствует, если некоторое 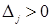 , но среди чисел
, но среди чисел 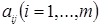 нет положительных (т.е. целевая функция не ограничена на множестве ее планов).
нет положительных (т.е. целевая функция не ограничена на множестве ее планов).
Замечание 2. Задача по нахождению 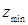 сводится к нахождению
сводится к нахождению 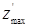 . Для этого достаточно изменить коэффициенты целевой функции
. Для этого достаточно изменить коэффициенты целевой функции 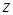 на противоположные (
на противоположные (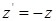 ) и решать задачу по нахождению максимума функции, при этом ограничения оставить прежними.
) и решать задачу по нахождению максимума функции, при этом ограничения оставить прежними.
 2015-08-21
2015-08-21 194
194






