Основные понятия и алгоритм стандартного симплекс-метода

Пусть стоит задача максимизации (минимизации)

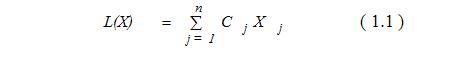
при условиях

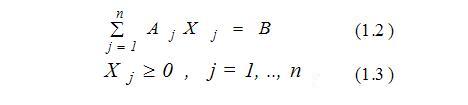
где Aj (j=1,...,n), B - m-мерные векторы.

Напомним несколько ключевых определений и свойств задачи.

Вектор X=(X1,X2,..,Xn), удовлетворяющий условиям (1.2) и (1.3), называется планом. Множество планов в геометрической интерпретации представляет собой выпуклый многогранник.

План, который обращает в равенство хотя бы n независимых ограничений задачи, называется опорным планом. Опорный план соответствует некоторой вершине многогранника планов.

Опорный план содержит не свыше m положительных компонент (m - число независимых ограничений задачи). Опорный план, содержащий менее m положительных компонент, называют вырожденным.

Оптимальный план является опорным (если оптимум достигается на двух опорных планах, то оптимальны все планы, соответствующие отрезку, соединяющему соответствующие вершины).

Система m векторов Aj при положительных компонентах опорного плана называется базисом этого плана.

Симплекс- метод - это метод упорядоченного перебора опорных планов. Упорядоченность в данном случае обеспечивается последовательным перебором опорных планов с монотонным изменением значения целевой функции в сторону возрастания (убывания).

В теоретическом обосновании симплексного метода [1] обнаруживается, что в случае единичного базиса (векторы образуют единичную матрицу) коэффициенты разложения некоторого вектора по векторам базиса, используемые в симплексной процедуре, совпадают с компонентами самого вектора (в общем же случае придется решать систему уравнений). Поэтому на практике стремятся иметь дело с единичным базисом.

Предположим, что исходная задача приведена к канонической форме (1.1)-(1.3) при В 0 и первые m векторов начального базиса образуют единичную матрицу (их можно принять за базис).

Для единообразия описания вычислительной процедуры в дальнейшем будем пользоваться т. н. симплексными таблицами вида:

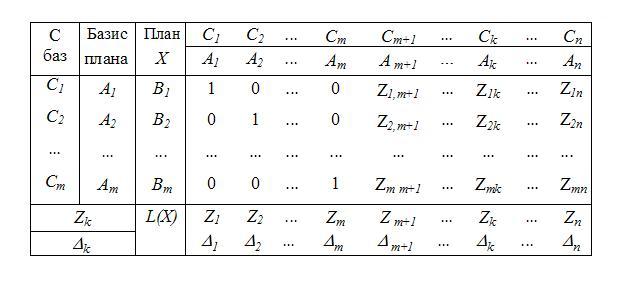
В первом столбце таблицы (С баз) записывают коэффициенты целе-вой функции (С1, С2 …Сm) при базисных переменных (напомним, что в базис входят только векторы, образующую единичную подматрицу, как в нашем случае А1 / Аm). Во втором столбце (Базис плана) должны нахо-диться базисные векторы данного опорного плана, а в третьем столбце (План Х) - правая часть ограничений задачи (базисные компоненты плана). Таким образом, перемножая элементы первого столбца таблицы со столбцом - "План Х", и суммируя эти произведения, мы получаем значе-ние целевой функции (ячейка - L(X)=С1*В1 + С2*В2+…+ +Сm*Bm).

Первая строка симплексной таблицы содержит коэффициенты ли-нейной функции нашей задачи и остается неизменной на протяжении все-го решения (С1, С2, …, Сn).

В центральной части таблицы записывают коэффициенты при неиз-вестных в ограничениях исходной задачи (Z11,…, Z1n,…, Zm1,…, Zmn). При этом следует заметить, что коэффициенты при базисных переменных в ограничениях задачи составляют единичную подматрицу.
Строку Zk рассчитывают по формуле

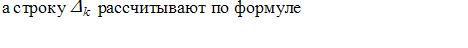
Известно, что при переходе к новому опорному плану X(Θ), в котором k-я компонента равна Θ>0 (станет базисной), значение целевой функции изменится и будет равно

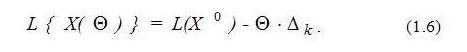
Выводы относительно данного опорного плана делают на основании содержимого последней строки таблицы по следующим критериям.

Критерий 1 (критерий оптимальности). Если все Δk >= 0, то выбранный план для задачи максимизации является оптимальным (для задачи на минимум признак оптимальности - неположительность всех Δk).

Критерий 2. Если обнаруживается некоторое Δk < 0 (для задачи минимизации Δk>0) и хотя бы одно из значений Zjk >0, то переход к новому опорному плану увеличит (уменьшит) значение целевой функции. При этом в базис будет вводиться новый вектор, выбор которого определяется по критерию максимального по модулю произведения Θ*Δk. Ес-ли к тому же учесть, что число положительных (базисных) компонент опорного плана должно оставаться равным m, то одну из m базисных компонент исходного плана обращаем в нуль выбором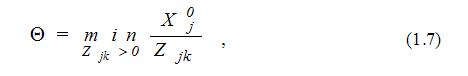
где X_j^o- компоненты опорного плана;
Z_jk- коэффициенты при k-й переменной в ограничениях задачи.

Критерий 3. Если обнаруживается некоторое Δk < 0, но все Zjk<=0, то линейная форма задачи не ограничена по максимуму (неограничен-ность по минимуму устанавливается аналогично при Δk>0 и всех Zjk <=0).

Переход к очередной симплексной таблице сводится к тому, чтобы выразить Xk из уравнения, соответствующего минимуму для Θ, и исключить из остальных уравнений (в итоге получаем единичный вектор при новой базисной компоненте и тем самым сохраняется единичная подматрица при базисных векторах):

1. Строку, соответствующую вектору, выводимому из базиса (главная строка), делим на коэффициент (главный элемент), находящийся на пересечении этой строки и столбца, соответствующего вектору, вводимому в базис (главный столбец).

2. От всех остальных строк вычитаем преобразованную главную строку, умноженную на элемент, находящийся на пересечении искомой строки и главного столбца.

Получив новую симплексную таблицу для улучшенного опорного плана, действуем по той же схеме, т.е. проверяем новый план на оптимальность и при необходимости переходим к очередному опорному плану. Этот процесс продолжаем до тех пор, пока найденный опорный план не окажется оптимальным.