Пример 1

Предприятие планирует закупить четыре вида сырья, которое должно использоваться на производство продукции А, Б, В в следующих про-порциях:

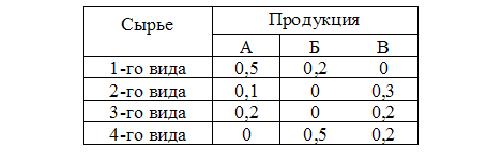
У предприятия имеются заказы на поставку этих видов продукции в размерах до 10, 30 и 20 единиц соответственно. В договоре предусмотрены цены поставок за единицу продукции - 10, 8 и 20 условных единиц. Рыночная цена требуемого предприятию сырья равна 2, 5, 8 и 3 у.е. за единицу сырья соответственно.

Необходимо определить объем закупаемого сырья, чтобы прибыль от реализации готовой продукции была максимальной.

Решение:

Для начала нам необходимо привести задачу к такому виду, чтобы мы могли определиться с методом ее решения.

1 этап. Математическая постановка задачи

В начале определим, какие величины в задаче неизвестны и что нужно найти. Так как нам необходимо определить оптимальное количество закупаемого сырья, обозначим за Х1, Х2, Х3 и Х4 - объемы закупки сырья соответствующих видов. В этом случае количество произведенной продукции будет равняться:
- продукции А - 0,5Х1+0,1Х2+0,2Х3;
- продукции Б - 0,2Х1+0,5Х4;
- продукции В - 0,3Х2+0,2Х3+0,2Х4.

Прибыль от реализации продукции сложится из выручки от продажи произведенной продукции за вычетом затрат на покупку необходимого сырья. Тогда данная задача запишется в виде:

Максимизировать

L(X)=10(0,5X1+0,1X2+0,2X3)+8(0,2Х1+0,5Х4)+
+20(0,3Х2+0,2Х3+0,2Х4)-(2X1+5X2+8X3+3X4)

при ограничениях

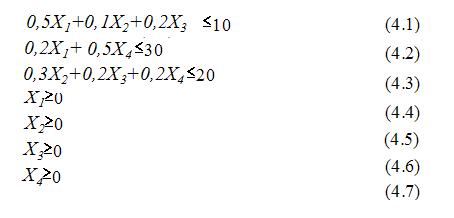
Условия (4.1)-(4.3) - это ограничения на объем производства продукции типа А, Б, В. При их построении мы исходили из предположения, что не имеет смысла производить больше продукции, чем мы можем реализовать.

Условия (4.4)-(4.7) - естественные условия неотрицательности переменных (объемы закупки сырья не могут быть отрицательны).

В итоге мы имеем оптимизационную задачу с четырьмя неизвестными и семью ограничениями (четырьмя ограничениями на неотрицательные неизвестные).

2 этап. Приведение задачи к каноническому виду

В соответствии с требованиями, которые были описаны выше, нам необходимо представить ограничения (4.1)-(4.3) в виде равенств. Для этого введем ослабляющие переменные со знаком (+), так как в ограниче-ниях знак (<=), и для простоты последующей работы приведем подобные члены в целевой функции. Тогда задача примет вид:

Максимизировать

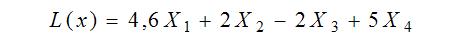
при ограничениях

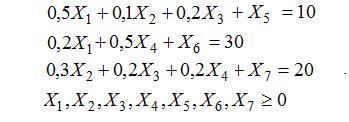
Таким образом, получена задача с 7 неизвестными и 10 ограничениями, допускающая решение стандартным симплекс-методом.

3 этап. Выбор начального опорного плана

Для простоты выбора базисных векторов и начального плана представим нашу исходную задачу в матричной форме.
С = {4,6, 2, -2, 5, 0, 0, 0} - вектор коэффициентов при переменных задачи в целевой функции.
В = {10, 30, 20} - вектор значений правых частей ограничений задачи.

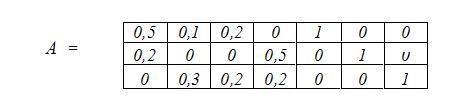
- матрица коэффициентов при переменных в ограничениях задачи.

Как мы видим, в матрице А присутствует единичная подматрица, которая соответствует векторам А5, А6, А7, следовательно, начальный опорный план будет выглядеть так: Х0 ={0, 0, 0, 0, 10, 30, 20}.

4 этап.Решение задачи симплекс-методом

Строим начальную симплексную таблицу и проверяем начальный опорный план Х0 на оптимальность. Начальный базис Б0=(А5, А6, А7)

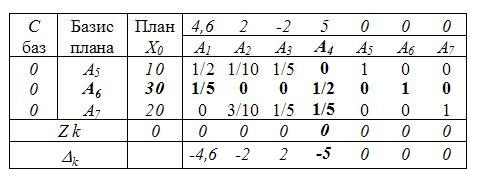
Из таблицы видно, что начальный опорный план не оптимален (для нашей задачи на максимум обнаруживаются отрицательные Δk и к тому же имеются значения Zjk >0). Следовательно, можно найти более хороший план. Для этого определяем вектор, вводимый в базис, и вектор, выводимый из базиса.

Так как при переходе к новому опорному плану значение целевой функции изменится и будет равно

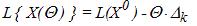
то очевидно желание вводить в базис вектор, для которого Δk<0 и величина /Θ*Δk/ наибольшая (последнее необязательно, но часто ускоряет достижение поставленной цели).Напомним, что

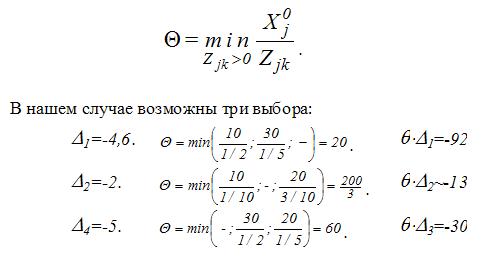
Разумно ввести в базис A4 вместо A6 (выражаем X4 из второго уравнения и исключаем из остальных).

Новая симплексная таблица для Б1=(А5, А4, А7) будет выглядеть следующим образом: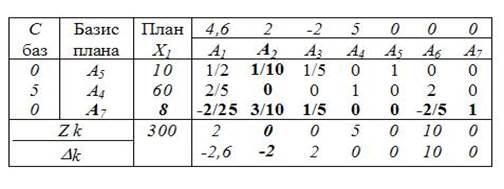
Полученный опорный план не оптимален, следовательно, необходимо его улучшить. Снова рассчитываем

В результате в базис войдут векторы: Б2=(А5, А4, А2). Строим новую симплексную таблицу.

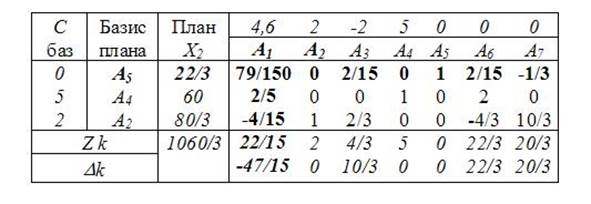
Очевидно, что найденный опорный план не оптимален, следовательно, необходимо его улучшить за счет ввода в базис вектора A1. Здесь

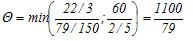
и из базиса выводится A5. Строим новую симплексную таблицу.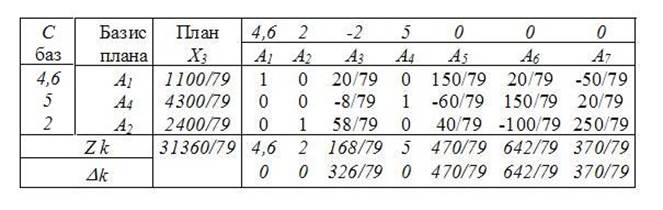

Из полученной таблицы видно, что найденный опорный план оптимален для данной задачи (все Δk >=0), т.е.
Хопт=(1100/79; 2400/79; 0; 4300/79) и Lmax = 31360/79.

Ответ для нашей задачи будет выглядеть следующим образом: для того, чтобы прибыль от производства и реализации продукции трех видов была максимально возможной при данных условиях, необходимо заку-пить сырье 1-го вида в объеме - ~ 13,92 единицы; сырье 2-го вида - ~ 30,38 единицы; сырье 3-го вида не закупать вовсе; сырье 4-го вида - ~ 54,43 единицы. В результате подобной политики мы получим прибыль в размере ~396,96 у.е.

Замечание. Как мы уже говорили неоднократно, при переходе к новому опорному плану значение целевой функции изменяется на величину

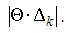
Следовательно, получив оптимальный план и обнаружив существование Δk=0, не соответствующего базисным векторам, можно сделать вывод, что найденный оптимальный план не единственный (можно перейти к другому плану с тем же значением целевой функции).