Для уравнений эллиптического типа
Исследования стационарных процессов различной физической природы (теплопроводность и др.) часто приводят к уравнениям эллиптического типа
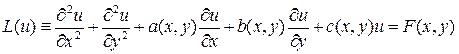 , (5)
, (5)
где 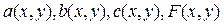 – непрерывные функции. Для этих уравнений обычно ставятся лишь краевые задачи, так как задачи Коши для эллиптического уравнения может быть некорректной. Наиболее часто встречаются следующие краевые задачи:
– непрерывные функции. Для этих уравнений обычно ставятся лишь краевые задачи, так как задачи Коши для эллиптического уравнения может быть некорректной. Наиболее часто встречаются следующие краевые задачи:
1. Первая краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция  . Требуется найти функцию
. Требуется найти функцию  , удовлетворяющую внутри G уравнению (42) и принимающую на границе заданные значения
, удовлетворяющую внутри G уравнению (42) и принимающую на границе заданные значения 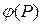 , т.е. должны быть выполнены условия
, т.е. должны быть выполнены условия 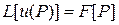 при
при 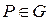 ;
; 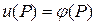 при
при  .
.
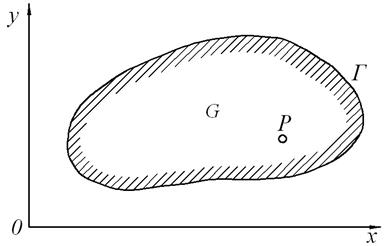
Рис. 4. Область исследования
2. Вторая краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция  . Требуется найти функцию
. Требуется найти функцию  , удовлетворяющую внутри G уравнению (42), нормальная производная которой на Г принимает заданные значения
, удовлетворяющую внутри G уравнению (42), нормальная производная которой на Г принимает заданные значения 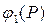 , т.е. требуется чтобы
, т.е. требуется чтобы 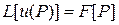 при
при 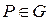 ;
; 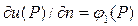 при
при 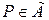 .
.
3. Третья краевая задача. На контуре Г, ограничивающем область G (рис. 4), задана непрерывная функция 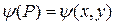 . Требуется найти функцию
. Требуется найти функцию 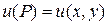 , такую, чтобы
, такую, чтобы 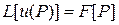 при
при 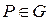 ;
; 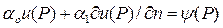 при
при  , где
, где 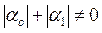 .
.
Третья краевая задача может быть рассмотрена как общая. Действительно, при 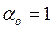 и
и 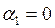 получаем первую краевую задачу, а при
получаем первую краевую задачу, а при 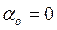 и
и 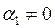 получаем вторую краевую задача. Если область G ограничена, то соответствующая краевая задача называется внутренней, а в противном случае – внешней. Для уравнения Лапласа
получаем вторую краевую задача. Если область G ограничена, то соответствующая краевая задача называется внутренней, а в противном случае – внешней. Для уравнения Лапласа 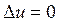 первая краевая задача называется задачей Дирихле, вторая – задачей Неймана и третья – смешанной краевой задачей.
первая краевая задача называется задачей Дирихле, вторая – задачей Неймана и третья – смешанной краевой задачей.
Применение метода сеток для решения задачи Дирихле
Идея метода сеток (метода конечных разностей) для численного решения краевых задач для двумерных дифференциальных уравнений заключается:
1) в плоскости G, в которой разыскивается решение, строится сеточная область  , состоящее из одинаковых ячеек и приближающая данную область G;
, состоящее из одинаковых ячеек и приближающая данную область G;
2) заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением;
3) на основании граничных условий устанавливаются значения искомого решения в граничных узлах области  .
.
Решив полученную систему конечно-разностных уравнений (т.е. систему алгебраических уравнений с большим числом неизвестных), мы найдем значения искомой функции в узлах сетки.
Сеточная область может состоять из квадратных, прямоугольных, треугольных и других клеток. От выбора основного размера клетки h зависит величина погрешности. Обычно задача решается сначала при большом значении h (малом числе клеток), а затем после грубого решения переходят к более мелкой сетке или во всей рассматриваемой области, или в какой-нибудь ее перспективной части.
Покажем применение метода сеток для построения решения задачи Дирихле
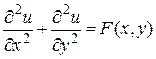 при
при 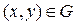 и
и 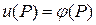 при
при 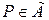 , (6)
, (6)
где 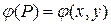 – заданная непрерывная функция (граничные условия).
– заданная непрерывная функция (граничные условия).
Для простоты рассмотрим лишь случай квадратной сетки. Будем предполагать также, что область G ограничена простым замкнутым кусочно-гладким контуром Г.
Выбрав шаг h, построим квадратную сетку 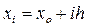 ,
, 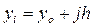 с таким расчетом, чтобы узлы (
с таким расчетом, чтобы узлы (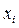 ,
, 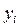 ) сетки
) сетки 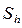 или принадлежали области G, или отстояли от ее границы Г на расстояние меньше, чем h.
или принадлежали области G, или отстояли от ее границы Г на расстояние меньше, чем h.
Узлы сетки 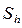 называются соседними, если они удалены друг от друга в направлении оси Оx или Oy на расстояние, равное шагу сетки h. Узел
называются соседними, если они удалены друг от друга в направлении оси Оx или Oy на расстояние, равное шагу сетки h. Узел 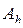 называется внутренним, если он принадлежит области G, а все четыре соседних с ним узла – множеству
называется внутренним, если он принадлежит области G, а все четыре соседних с ним узла – множеству 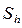 , в противном случае он называется граничным (например, узлы
, в противном случае он называется граничным (например, узлы  и
и  сетки
сетки  ). На рис. 5 внутренние узлы обозначены светлыми кружками, а граничные темными кружками и треугольниками.
). На рис. 5 внутренние узлы обозначены светлыми кружками, а граничные темными кружками и треугольниками.
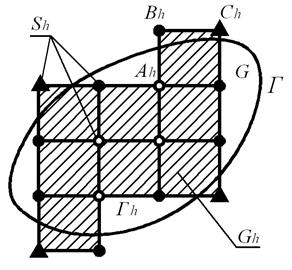
Рис. 5. Узлы сетки 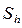
Граничный узел сетки 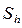 называется узлом первого рода, если он имеет соседний внутренний узел этой сетки (например, узел
называется узлом первого рода, если он имеет соседний внутренний узел этой сетки (например, узел 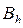 на рис. 5); в противном случае граничный узел называется узлом второго рода (узел
на рис. 5); в противном случае граничный узел называется узлом второго рода (узел 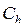 на рис. 5). Внутренние узлы и граничные узлы первого рода сетки
на рис. 5). Внутренние узлы и граничные узлы первого рода сетки 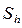 называются расчетными точками. Граничные узлы второго рода не входят в вычисление и могут быть изъяты из сетки
называются расчетными точками. Граничные узлы второго рода не входят в вычисление и могут быть изъяты из сетки 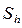 (на рис. 5 граничные узлы второго рода обозначены темными треугольниками).
(на рис. 5 граничные узлы второго рода обозначены темными треугольниками).
Относительно сетки 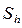 предположим, что множество ее расчетных точек «связное», т. е. любые две расчетные точки можно соединить цепочкой узлов, каждые два смежных элемента которой являются соседними узлами. Кроме того, будем считать многоугольную сеточную область
предположим, что множество ее расчетных точек «связное», т. е. любые две расчетные точки можно соединить цепочкой узлов, каждые два смежных элемента которой являются соседними узлами. Кроме того, будем считать многоугольную сеточную область 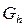 выбранной так, чтобы ее геометрическая граница
выбранной так, чтобы ее геометрическая граница 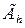 , возможно ближе примыкала к границе Г области G. Заметим, что узловые точки контура
, возможно ближе примыкала к границе Г области G. Заметим, что узловые точки контура 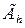 могут лежать как внутри, так и вне области G.
могут лежать как внутри, так и вне области G.
Значение искомой функции и=и(х,у) в точках 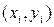 обозначим через
обозначим через 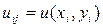 . Следуя общей схеме, для каждой внутренней точки
. Следуя общей схеме, для каждой внутренней точки 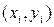 сетки
сетки 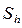 заменяем дифференциальное уравнение (6) конечно-разностным уравнением
заменяем дифференциальное уравнение (6) конечно-разностным уравнением
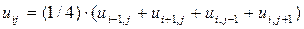 , (7)
, (7)
где 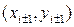 – расчетные точки.
– расчетные точки.
В граничных узлах первого рода 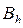 полагаем
полагаем 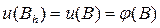 ,
,
где B – ближайшая к 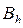 точка границы Г.
точка границы Г.
Система (7) является неоднородной системой, причем число неизвестных (т.е. число внутренних узлов сетки) равно числу уравнений. Решив систему (7), получим приближенные значения искомой функции и=и(х,у) в узлах сеточной области 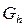 . Тем самым будет найдено приближенной решение задачи Дирихле для области
. Тем самым будет найдено приближенной решение задачи Дирихле для области 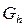 .
.
Если число узлов сетки 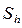 велико, а также с учетом криволинейности области G для решения системы (7) прибегают к итерационным методам, с одновременным исправлением граничных значений. Так согласно процессу усреднения Либмана, выбрав начальное приближение
велико, а также с учетом криволинейности области G для решения системы (7) прибегают к итерационным методам, с одновременным исправлением граничных значений. Так согласно процессу усреднения Либмана, выбрав начальное приближение 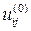 , последовательные приближения
, последовательные приближения 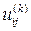 для внутренних узлов
для внутренних узлов 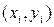 сетки
сетки 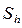 определяем по формуле
определяем по формуле
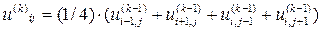 (k=1,2,…). (8)
(k=1,2,…). (8)
 2015-08-12
2015-08-12 974
974








