Лабораторная работа № 5
ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХНЫХ
УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ.
ЗАДАЧА ДИРЕХЛЕ ДЛЯ ЭЛИПТИЧЕСКОГО УРАВНЕНИЯ.
Цель работы
1. Знакомство с методами численного решения дифференциальных уравнений с частными производными в рамках задачи Дирехле.
2. Разработка численной ММ, реализующей один из методов.
3. Оценка точности полученной ММ при помощи средств MATLAB.
Решение дифференциальных уравнений с частными производными (ДУЧП) в аналитическом виде удается только в самых простых случаях. Поэтому становятся особенно важными численные (приближенные) методы решения этих уравнений. Далее будем рассматривать только линейные ДУЧП.
Наиболее широко распространенным и простым методом численного решения линейных ДУЧП является метод сеток или метод конечных разностей, поэтому основной упор сделан на пояснение и описание этого метода.
В общем случае ДУЧП для функции u двух аргументов имеет вид
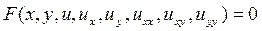 , (1)
, (1)
где x, у – независимые переменные, u(x,y) – искомая функция, ux, uy, uxx, uxy, uyy – её первые и вторые частные производные по аргументам x и y.
Решением уравнения (1) называется функция и= u(х, у), обращающая это уравнение в тождество. График решения представляет собой поверхность в пространстве Охуu (интегральная поверхность).
Уравнение (1) называется вполне линейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, т. е. если это уравнение может быть записано в виде
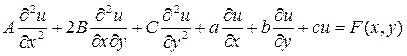 , (2)
, (2)
причем коэффициенты А, В, С, а, b, с могут зависеть лишь от х и у. В частном случае, если эти коэффициенты не зависят от х и у, то уравнение (2) будет линейным дифференциальным уравнением с постоянными коэффициентами. Подробнее рассмотрим линейное дифференциальное уравнения (2).
Пусть D= В2-4АС – дискриминант уравнения. В зависимости от знака функции D линейное дифференциальное уравнение (2) относится в заданной области к одному из следующих типов:
D < 0 – эллиптический тип; D = 0 – параболический тип;
D > 0 – гиперболический тип; D не сохраняет постоянного знака – смешанный тип.
Например, температура и=и(х, у) точки (х,у) пластинки при стационарном распределении (т. е. при распределении, не зависящем от времени) и отсутствии источников тепла удовлетворяет уравнению Лапласа вида:
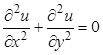 (3)
(3)
Для этого уравнения А=1, В=0, С=1 Тогда дискриминант D= В2-4АС <0 поэтому уравнение (3) эллиптического типа
Уравнения Лапласа в конечных разностях
Для получения конечно-разностного уравнения, соответствующего уравнению Лапласа (частный случай уравнения эллиптического типа) достаточно, выбрав шаг h>0, заменить производные отношениями конечных разностей по формулам:
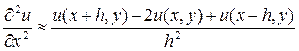 и
и 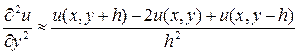 .
.
Тогда после преобразования будем иметь
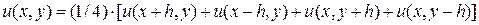 . (4)
. (4)
 2015-08-12
2015-08-12 530
530







