Сделаем содержательную постановку задачи. В объединении находится n автомобилей, способных каждый перевозить в месяц Qi тонн груза (i = 1,2,…,n). С их помощью необходимо обеспечить перевозку грузов (пиломатериал, шурупы и т.д.) от поставщиков к потребителям по n маршрутам в количестве Rj тонн в месяц (j = 1,2,…,n).
Распределить автомобили по маршрутам так, чтобы минимизировать суммарную величину неиспользуемой провозной способности. Конкретизируем задачу (рис. 1). Пусть имеется 4 автомобиля и 4 маршрута. Характеристики провозных способностей автомобилей соответственно равны Q1 = 30 т., Q2 = 35 т., Q3 = 5 т., Q4 = 5 т. Характеристики потребностей потребителей соответственно равны R1 = 25 т., R2 = 32 т., R3 = 5 т., R4 = 4 т. Задача заключается в том, чтобы перевезти все грузы с минимальными издержками, для этого надо каждый автомобиль пустить по одному и только его маршруту. Понятно, если возможность автомобиля в перевозке груза ниже потребности потребителя этого груза, то на данный маршрут автомобиль не может быть назначен. Поэтому составим матрицу С, характеризующую издержки i -го автомобиля, в случае, если он будет назначен на j -й маршрут. Элементы маршрута будут равны:
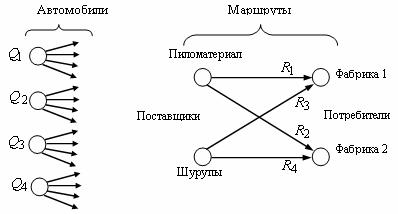
Рис. 1 - Схема маршрутов
В таблице 1 приводятся оценки возможных транспортных издержек.
Таблица 1 - Оценки транспортных издержек
| Rj Qi | 25 | 32 | 5 | 4 |
| 30 | 5 | М | 25 | 26 |
| 35 | 10 | 3 | 30 | 31 |
| 5 | М | М | 0 | 1 |
| 5 | М | М | 0 | 1 |
Сделаем математическую постановку задачи о назначениях.
Переменные. В качестве переменной введем величину

Ограничения. Каждый автомобиль i должен быть назначен только один раз на любой из маршрутов.
или.
На каждый маршрут j должен быть назначен один из автомобилей
или.
Целевая функция. В качестве целевой функции, подлежащей минимизации, выступают суммарные издержки на перевозку.
Модель задачи о назначениях примет вид:
при ограничениях:,
,
.
Все предполагаемые алгоритмы поиска решения задачи о назначениях базируются на следующем утверждении: оптимальное решение задачи не изменится, если к любой строке или столбцу матрицы издержек прибавить (или вычесть) постоянную величину в силу того, что приоритет назначения не изменится. И весь алгоритм ведется на матрице издержек с соответствующими преобразованиями для получения в ней нулевых элементов, образующих систему так называемых «независимых нулей». Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке.
(1)
Как только будут получены нулевые элементы, применяют различные алгоритмы: Мака, венгерский, минимальных линий. Рассмотрим процедуру вычеркивания нулевых элементов минимальным числом прямых линий. В матрице 2 показано, как используется это правило. Могут быть и другие варианты вычеркивания.
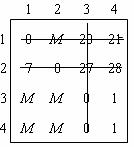
Если все нулевые элементы в матрице будут вычеркнуты, а минимальное число линий будет равно размерности матрицы, то независимые нули в матрице существуют, и решение найдено. В противном случае выбирается наименьший элемент из невычеркнутых элементов (он равен 1). Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
В результате получается матрица (3), которая указывает на два оптимальных решения (матрицы решений 4 и 5).
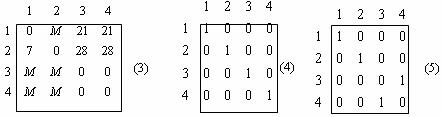
Значение целевой Z = 5 + 3 + 0 + 1 = 9. Оптимальное решение можно было получить и сразу, не применяя процедуру вычеркивания нулей, если в матрице 2 из столбца 4 вычесть минимальный элемент. Сделано было иначе только для демонстрации процедуры вычеркивания.
Следует заметить, что, если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
15 вопрос.
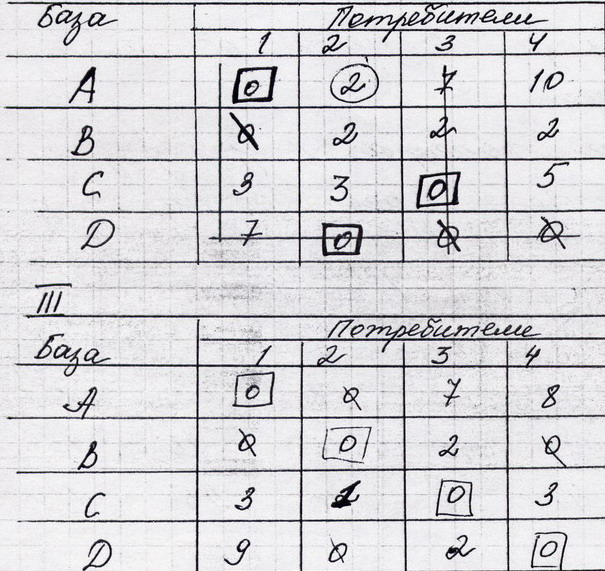
Задача о назначениях - частный случай транспортной задачи, в которой количество пунктов производства и потребления равны, т.е транспортная таблица имеет форму квадрата, а объем потребления и производства в каждом пункте равен 1. Данная задача решается с помощью алгоритма, носящего название "Венгерского метода", состоящего из 3 этапов: 1 этап: 1 Формализация проблемы в виде транспортной таблицы 2 В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки 3 Повторить ту же процедуру для столбцов Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой стоимостью. Оптимальное значение целевой функции в этом случае равно нулю. 2 этап: 1 Найти строку, содержащую только одно нулевое значение, в его клетку помещается один элемент (0 обводится квадратиком). Если такие строки отсутствуют, допустимо начать с любой строки. 2 Зачеркнуть оставшиеся нулевые значения данного столбца 3 Повторять пп.1-2, пока продолжение указанной процедуры окажется невозможным Если окажется, что имеется несколько нулей, которым не соответствуют назначения, и которые остались незачеркнутыми, необходимо: 4 Найти столбец, содержащий только одно нулевое значение, в его клетку помещается один элемент. 5 Зачеркнуть оставшиеся нули в данной строке 6 Повторять пп.4-5, пока продолжение указанной процедуры окажется невозможным Если выяснится, что таблица содержит неучтенные нули - повторить пп. 1-6 Если решение является допустимым, оно оптимально. Если нет - перейти к этапу 3. 3 этап: (Если решение является недопустимым) 1 Провести минимальное количество прямых через столбцы и строки матрицы таким образом, чтобы они проходили через все нули, содержащиеся в таблице 2 Найти наименьший из элементов, через которые не проходит ни одна прямая 3 Вычесть его из всех элементов, через которые не проходят прямые 4 Прибавить его ко всем элементам, лежащим на пересечении прямых 5 Элементы, через которые проходит только одна прямая, оставить неизменными В результате в таблице появится как минимум одно новое нулевое значение. Вернуться к этапу 2 и повторить решение заново. Пример решения задачи Компания имеет 4 сбытовых базы и 4 заказа, которые необходимо доставить потребителям. Складские помещения каждой из баз достаточны для размещения любого из этих заказов. Составим транспортную таблицу.
Вычтем минимальные элементы по строкам (выделены полужирным), получим новую таблицу:
Повторим ту же процедуру для столбцов:
На рисунке ниже приведено окончательное решение задачи. |
 2015-09-07
2015-09-07 762
762