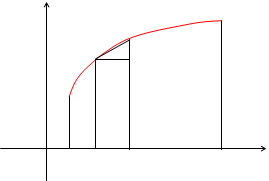
 y y = f(x)
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как 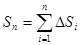 .
.
Тогда длина дуги равна 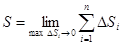 .
.
Из геометрических соображений: 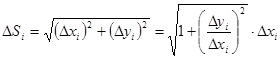
По теореме Лагранжа имеем 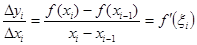 , где
, где 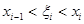
Следовательно 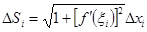
Таким образом, длина вписанной ломаной равна
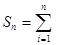
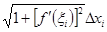
По условию 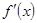 - непрерывна, следовательно, функция
- непрерывна, следовательно, функция 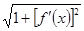 тоже непрерывна. Поэтому существует предел интегральной суммы, который равен определённому интегралу:
тоже непрерывна. Поэтому существует предел интегральной суммы, который равен определённому интегралу:
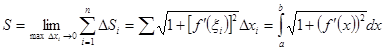
Итак, получили формулу для вычисления длины дуги:
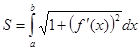 =
= 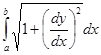 (9)
(9)
Если уравнение кривой задано параметрически х = j(t) и у = y(t),
 , где j(t) и j(t)- непрерывные функции с непрерывными производными, причём
, где j(t) и j(t)- непрерывные функции с непрерывными производными, причём  на заданном участке не обращается в ноль. В этом случае уравнения х = j(t) и у = y(t) определяют некоторую функцию
на заданном участке не обращается в ноль. В этом случае уравнения х = j(t) и у = y(t) определяют некоторую функцию 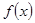 , непрерывную и имеющую непрерывную производную
, непрерывную и имеющую непрерывную производную 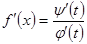 , пусть
, пусть 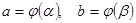 , тогда, сделав в интеграле (9) подстановку
, тогда, сделав в интеграле (9) подстановку 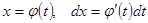 , получим
, получим 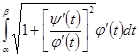 или
или
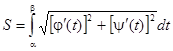 ,
,
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

Если кривая задана в полярных координатах, то
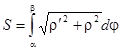 , r = f(j).
, r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
|
|
|
1 способ. Выразим из уравнения переменную у. 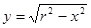
Найдем производную 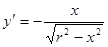
Тогда 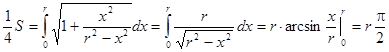
Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r, 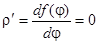 тогда
тогда
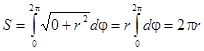
 2015-09-07
2015-09-07 440
440






