Треугольник Паскаля

4 5 6 7 8 9 10

ФРАКТАЛЬНАЯ ГРАФИКА

Понятие фрактала и история появления фрактальной графики. Понятие размерности и ее расчет.

Геометрические фракталы. Алгебраические фракталы. Системы итерируемых функций. Стохастические фракталы.

Математика,

Если на нее правильно посмотреть,

Отражает не только истину,

Но и несравненную красоту.

(Бертран Рассел)

Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется.

Фрактальные свойства объектов известны более 100 лет. Однако подробное изучение фракталов началось не более 30-35 лет назад. Родоначальниками теории фракталов являются математики.

Треугольник Паскаля

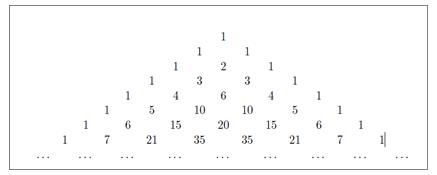
Очень легко продолжить треугольник, заметив, что каждое число в нем является суммой двух других, стоящих над ним.

Заменим в треугольнике Паскаля числа остатком от деления на 2 (mod 2): нечетные числа – единицей, а четные – нулем, закрасим пиксели

При стремлении количества рядов фигуры N к бесконечности, отображаемая фигура будет стремиться к некоторому пределу, который называется Ковер Серпинского и был открыт польским математиком Вацлавом Серпинским в 1916 году.

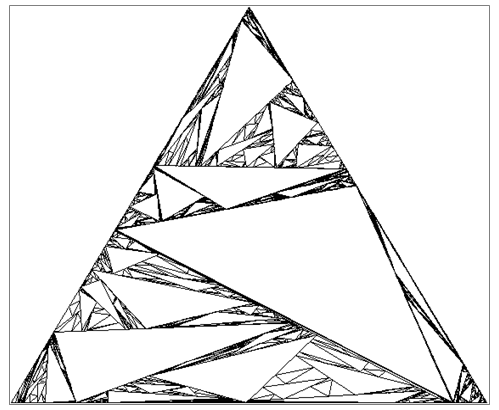
Алгоритм треугольника чрезвычайно прост: каждая сторона равностороннего треугольника делится пополам, соединяются полученные вершины, и снова весь процесс повторяется. Если делить отрезки не пополам, а в некотором отношении (т.е. соединять не середины отрезков, а некоторые другие точки), тогда мы получим нечто следующее http://fractalworld.xaoc.ru/Sierpinski_triangle:

Если на каждом шаге стороны треугольников разбивать случайным образом, то получится примерно следующее:

program FractSierp2; uses CRT, Graph; var gd, gm: Integer; const Iter = 8; procedure Tr(x1, y1, x2, y2, x3, y3: Real);begin Line(Round(x1), Round(y1), Round(x2), Round(y2)); Line(Round(x2), Round(y2), Round(x3), Round(y3)); Line(Round(x3), Round(y3), Round(x1), Round(y1))end; procedure Draw(x1, y1, x2, y2, x3, y3: Real; n: Integer);var x1n, y1n, x2n, y2n, x3n, y3n: Real; r, q: Real;begin if n > 0 then begin r:= Random; q:= Random; x1n:= (x1*r + x2*q) / (q+r); y1n:= (y1*r + y2*q) / (q+r); r:= Random; q:= Random; x2n:= (x2*r + x3*q) / (q+r); y2n:= (y2*r + y3*q) / (q+r); r:= Random; q:= Random; x3n:= (x3*r + x1*q) / (q+r); y3n:= (y3*r + y1*q) / (q+r); Tr(x1n, y1n, x2n, y2n, x3n, y3n); Draw(x1, y1, x1n, y1n, x3n, y3n, n - 1); Draw(x2, y2, x1n, y1n, x2n, y2n, n - 1); Draw(x3, y3, x2n, y2n, x3n, y3n, n - 1) endend; begin gd:= Detect; Randomize; InitGraph(gd,gm,'c:\bp\bgi'); repeat ClearDevice; Tr(320, 10, 600, 470, 40, 470); Draw(320, 10, 600, 470, 40, 470, Iter); until Readkey = #27; CloseGraphend.

Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, когда требуется с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого графического представления сложных неевклидовых объектов, образы которых весьма похожи на природные. В основе таких построений лежат геометрические фракталы, построенные по определенным алгоритмам.

Первые идеи фрактальной геометрии возникли в 19 веке. Георг Кантор (1845-1918) с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая «Пыль Кантора»). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками.

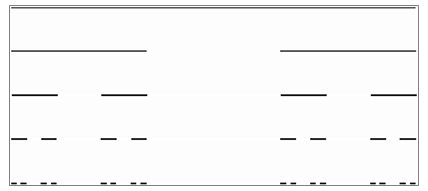
Рис.1

Нетрудно заметить, что суммарная длина получившихся в пределе отрезков равна нулю (размерность фигуры равна 0), так как мы исключили в результате длину, равную 1:

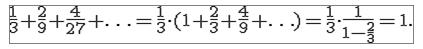
Существуют фракталы, которые плотно заполняют пространство, в котором они находятся. Одним из примеров такого рода являются кривые Пеано (Peano curves). Первая из них была найдена Пеано в 1890 г. Начальным (инициирующим) элементом здесь можно выбрать единичный квадрат, каждая из сторон которого на следующем шаге заменяется генератором, показанным на рисунке: