Выгоднейшая форма треугольников

ЧАСТОТА РАЗМЕЩЕНИЯ АЗИМУТОВ И БАЗИСНЫХ СТОРОН.

Согласование точности угловых и линейных измерений в геодезических сетях

Оценка точности линейно-угловых сетей и звеньев полигонометрии.

Частота размещения азимутов. Азимуты Лапласа играют важ­ную роль при создании опорных геодезических сетей: обеспе­чивают независимую азимутальную ориентировку сторон гео­дезической сети во всех ее частях, причем с одинаковой высо­кой точностью; позволяют контролировать результаты угловых измерений по невязкам азимутальных условий, ослабляя при этом влияние систематических ошибок измерений; приводят к возникновению азимутальных условных уравнений при уравнивании сети и тем самым способствуют повышению ее точности.

Рассчитаем предельно допустимое число треугольников п_тах, через которое необходимо размещать азимуты Лапласа в три­ангуляции, чтобы они могли выполнять функцию контроля уг­ловых измерений.

Пусть на концах цепочки треугольников изме­рены азимуты α ₁ и а₂. Используя промежуточные углы C_i тре­угольников, напишем в общем случае

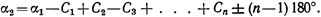
Перейдя к средним квадратическим ошибкам, получим

2т²_α= п т²,

где т_а и т - средние квадратические ошибки измерения ази­мутов и углов соответственно; n - число промежуточных углов, равное числу треугольников между азимутами.

Пусть заданы предельные значения ошибок: т_{а пред} = tm_a и n _пред. = п_тах. Тогда при заданном значении средней квадратической ошибки т" измерения углов и t=2,5, как это принято в геодезии при расчете допусков, найдем

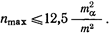
При т_а. =т получим n _mах=12; при т_а. = 1,0"и m = 0,7" - n _mах= 25.

Звенья триангуляции 1 класса состоят из 12-16 треуголь­ников. В сетях триангуляции 2 класса в соответствии с требо­ваниями инструкции азимуты должны определяться не более чем через 25 треугольников.

Частота размещения базисных сторон. Базисные стороны в триангуляции, как и азимуты Лапласа, играют важную роль. Они устанавливают единый масштаб построения геодезических сетей на земной поверхности; позволяют контролировать точ­ность передачи длин сторон, ослабляя при этом накопление си­стематических ошибок измерений; приводят к возникновению базисных условных уравнений при уравнивании геодезической сети и тем самым способствуют повышению ее точности.

В целях обеспечения стройной системы построения государ­ственной геодезической сети азимуты Лапласа принято опреде­лять на обоих концах базисных сторон. Поэтому в триангуля­ции частота размещения базисных сторон такая же, как азиму­тов Лапласа.

Выгоднейшая форма треугольников. В триангуляции любая сторона треугольника имеет одинаково важное значение, поэ­тому связующие S и промежуточные С стороны треугольников должны при прочих равных условиях определяться с одинако­вой высокой точностью. Это требование может быть записано в виде равенства

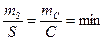
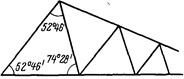
При реализации данного требования треугольники в рядах триангуляции получаются равнобедренными с углами С=А =52°46' и В=74⁰28'. Однако такая форма треугольников не пригодна для практики, поскольку в этом случае ряд «вырож­дается» по мере удаления от исходной базисной стороны. С практической точки зрения наиболее выгодными по форме являются равносторонние треугольники, построение ко­торых, однако, не всегда возможно вследствие особенностей рельефа местности. В рядах триангуляции 1 класса углы в тре­угольниках должны быть не менее 40°, а в сплошных сетях триангуляции 2 класса - не менее 30°.

с

. Схема цепи треугольников с «выгоднейшими» углами

А

в