Алгебраические фракталы

Свое название они получили за то, что их строят на основе алгебраических формул, иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции:

Z_n+1=f(Z_n),

где Z – комплексное число, а f – некая функция.

Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится – на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:

− с течением времени стремится к бесконечности;

− стремится к 0;

− принимает несколько фиксированных значений и не выходит за их пределы;

− поведение хаотично, без каких либо тенденций.

Классической иллюстрацией алгебраических фракталов является множество Мандельброта:

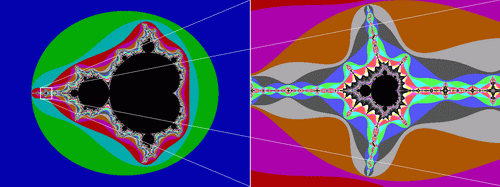
Рис. Множество Мандельброта

Для его построения нам необходимы комплексные числа. Комплексное число – это число, состоящее из двух частей – действительной и мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а bi – мнимая часть. i – называют мнимой единицей, потому, что если мы возведем i в квадрат, то получим –1.

Комплексные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень (исключение – операции сравнения).

Геометрическая интерпретация: комплексное число можно изобразить как точку на плоскости, у которой координата Х это действительная часть a, а Y это коэффициент при мнимой части b.

Для построения фрактала множества Мандельброта для всех точек на комплексной плоскости в интервале от (–2+2i) до (2+2i) выполняем некоторое достаточно большое количество раз: Z_n=Z₀*Z₀+C, каждый раз проверяя абсолютное значение Z_n. Если это значение | Z_n| > 2, то рисуем точку с цветом, равным номеру текущей итерации, иначе рисуем точку черного цвета (см. рис.).

Черный цвет в середине показывает, что в этих точках функция стремится к нулю – это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. Границы множества являются фрактальными, в этих точках функция ведет себя непредсказуемо – хаотично.

Меняя функцию условия выхода из цикла, можно получать другие фракталы. Например, взяв вместо выражения С=a+bi выражение Z₀=a+bi, присваивая величине С произвольные значения, мы получим множество Жюлиа. Выбирая для С случайные значения, получаем стохастический фрактал на основе множества Жюлиа.