Множество 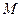 элементов
элементов 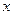 ,
, 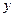 ,
, 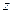 ,
,  называется группой, если определена бинарная операция
называется группой, если определена бинарная операция 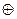 , которая каждой паре элементов
, которая каждой паре элементов 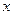 ,
, 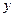 ставит в соответствие элемент
ставит в соответствие элемент 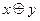 так, что выполняются свойства (аксиомы группы):
так, что выполняются свойства (аксиомы группы):
а) 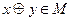 (замкнутость
(замкнутость 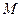 по отношению к операции
по отношению к операции 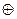 );
);
б) 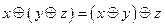 (ассоциативность операции
(ассоциативность операции 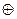 );
);
в) 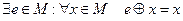 (существование нейтрального элемента);
(существование нейтрального элемента);
г) 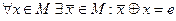 (существование обратного элемента для каждого элемента группы).
(существование обратного элемента для каждого элемента группы).
Группа 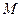 называется коммутативной (абелевой) если
называется коммутативной (абелевой) если 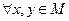
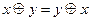 .
.
Множество 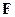
 элементов
элементов 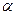 ,
, 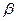 ,
, 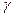 ,
, 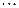 называется полем, если на нем определены две бинарные операции
называется полем, если на нем определены две бинарные операции 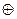 и
и 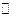 , условно называемые сложением и умножением, такие, что выполняются аксиомы поля:
, условно называемые сложением и умножением, такие, что выполняются аксиомы поля:
а) 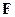 является коммутативной группой по сложению;
является коммутативной группой по сложению;
б) совокупность всех ненулевых элементов 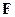 является коммутативной группой по умножению;
является коммутативной группой по умножению;
в) 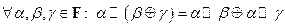 , (дистрибутивность сложения и умножения).
, (дистрибутивность сложения и умножения).
Множество 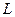 элементов
элементов 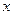 ,
, 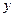 ,
, 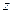 ,
, 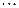 называется линейным (векторным) пространством над полем
называется линейным (векторным) пространством над полем 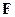 , а элементы множества
, а элементы множества 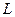 называются векторами, если на
называются векторами, если на 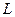 определены две бинарные операции – сложение векторов (+) и умножение вектора на скаляр (
определены две бинарные операции – сложение векторов (+) и умножение вектора на скаляр ( ), такие, что
), такие, что
I) 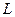 есть коммутативная группа по сложению векторов.
есть коммутативная группа по сложению векторов.
II) Операция умножения вектора (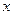 ,
, 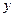 ,…) на скаляр (
,…) на скаляр (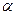 ,
, 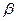 ,…) удовлетворяет следующим условиям:
,…) удовлетворяет следующим условиям:
а) 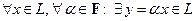 (замкнутость пространства относительно умножения вектора на скаляр);
(замкнутость пространства относительно умножения вектора на скаляр);
б) 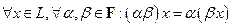 (ассоциативность умножения вектора на скаляр);
(ассоциативность умножения вектора на скаляр);
в) 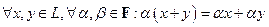 ,
, 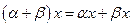 (дистрибутивность сложения векторов и умножения вектора на скаляр);
(дистрибутивность сложения векторов и умножения вектора на скаляр);
г) 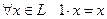 , где
, где 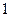 – элемент поля
– элемент поля 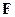 (скаляр), нейтральный относительно операции умножения скаляров в поле
(скаляр), нейтральный относительно операции умножения скаляров в поле 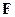 .
.
Метрикой (расстоянием) на произвольном множестве 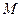 называется вещественная функция (или функционал[1])
называется вещественная функция (или функционал[1]) 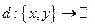 , определенная для любой пары элементов
, определенная для любой пары элементов 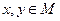 и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
а) 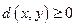 , и
, и 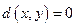 только если
только если 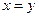 ;
;
б) 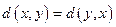 (симметрия);
(симметрия);
в) 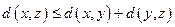 (неравенство треугольника).
(неравенство треугольника).
Множество 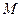 , на котором задана метрика
, на котором задана метрика 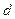 , называется метрическим пространством
, называется метрическим пространством 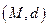 .
.
Пусть 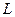 – линейное пространство над полем
– линейное пространство над полем 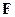 . Функция (функционал)
. Функция (функционал) 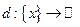 называется нормой вектора
называется нормой вектора 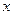 , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
а) 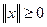 , причем
, причем 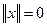 , только если
, только если 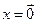 ;
;
б) 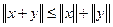 (неравенство треугольника);
(неравенство треугольника);
в) 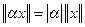 .
.
Пусть 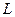 – линейное пространство над полем
– линейное пространство над полем 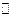 (или
(или 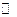 ). Функция (функционал)
). Функция (функционал) 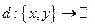 называется скалярным произведением, если она удовлетворяет следующим условиям:
называется скалярным произведением, если она удовлетворяет следующим условиям:
а) 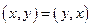 ;
;
б) 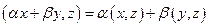 ;
;
в) 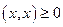 , причем
, причем 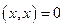 , только если
, только если 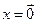 .
.
В пространстве со скалярным произведением выполняется неравенство Шварца
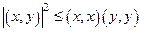 или
или 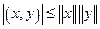 ,
,
на основе которого может быть введено понятие угла 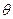 между векторами (только для пространства над полем
между векторами (только для пространства над полем 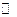 ), такого что
), такого что
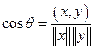 .
.
Совокупность векторов линейного пространства 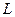 является линейно независимой, когда
является линейно независимой, когда 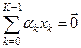 в том и только в том случае, если
в том и только в том случае, если 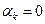 при всех
при всех 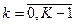 (здесь
(здесь 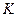 – количество векторов).
– количество векторов).
Если в пространстве 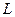 можно найти
можно найти 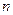 линейно независимых элементов, а любые
линейно независимых элементов, а любые 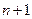 элементов этого пространства линейно зависимы, то пространство
элементов этого пространства линейно зависимы, то пространство 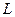 имеет размерность
имеет размерность 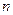 . Если в
. Если в 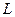 можно указать систему из произвольного конечного числа линейно независимых векторов, то говорят, что пространство
можно указать систему из произвольного конечного числа линейно независимых векторов, то говорят, что пространство 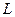 бесконечномерно.
бесконечномерно.
Базисом 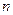 -мерного пространства
-мерного пространства 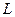 называется любая система из
называется любая система из 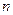 линейно независимых векторов. Базисом бесконечномерного пространства является бесконечная совокупность векторов, такая, что любое ее конечное подмножество линейно независимо.
линейно независимых векторов. Базисом бесконечномерного пространства является бесконечная совокупность векторов, такая, что любое ее конечное подмножество линейно независимо.
2. Прямое и обратное 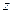 -преобразование
-преобразование
Прямое 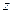 -преобразование последовательности
-преобразование последовательности 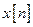 определяется выражением
определяется выражением
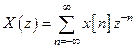 .
.
Обратное 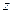 -преобразование
-преобразование
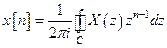 ,
,
где 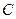 – контур, расположенный в области сходимости и охватывающий начало координат, направление обхода контура – против часовой стрелки.
– контур, расположенный в области сходимости и охватывающий начало координат, направление обхода контура – против часовой стрелки.
Теорема о вычетах:
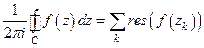 ,
,
где 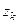 – изолированные полюсы, находящиеся внутри контура интегрирования. Если
– изолированные полюсы, находящиеся внутри контура интегрирования. Если 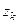 – полюс порядка
– полюс порядка 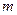 , то
, то
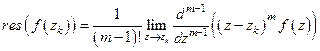 .
.
Свойства 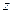 -преобразования:
-преобразования:
а) линейность
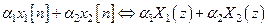
б) сдвиг последовательности
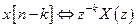
в) отражение последовательности
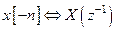
г) умножение на экспоненту
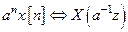
д) умножение на линейную последовательность
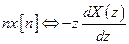
е) переход к комплексно-сопряженной последовательности
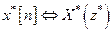
ж) свертка последовательностей
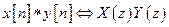
з) произведение последовательностей
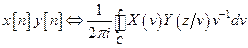
 2015-09-07
2015-09-07 604
604







