Прямое и обратное преобразование Фурье

Прямое преобразование Фурье определяется выражением

.

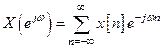Для абсолютно суммируемой последовательности 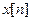ряд в правой части выражения сходится равномерно к непрерывной функции аргумента .

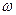Обратное преобразование Фурье определяется выражением

, .

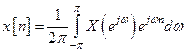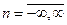Формулы Эйлера

,

,

.

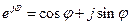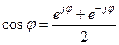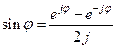Некоторые неравенства

,

,

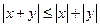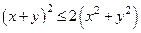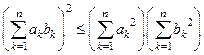– неравенство Коши – Буняковского (Шварца)

6. Свойства 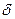-функции Дирака

а) 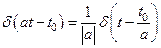, б) .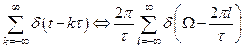

Формула суммирования Пуассона

.

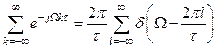Спектральные плотности некоторых сигналов

а) ,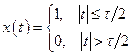

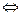
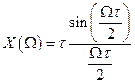б) ,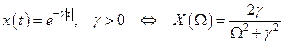

в) .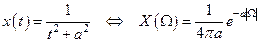

Некоторые числовые суммы

а) 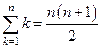, б) ,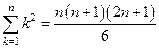

в) .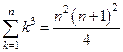

[1] Функционалом называется отображение множества функций на множество чисел. Примером функционала является определенный интеграл.