Можно доказать, что всякую матричную игру с нулевой суммой можно свести к паре разрешимых симметричных двойственных задач линейного программирования. Справедливо и обратное. Пара симметричных двойственных задач линейного программирования эквивалентна игре.
Рассмотрим игру, заданную матрицей: 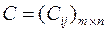 . Будем считать, что все элементы Cij > 0. Если это не так, то прибавим ко всем элементам матрицы C некоторое число M > 0 (Cij + M =
. Будем считать, что все элементы Cij > 0. Если это не так, то прибавим ко всем элементам матрицы C некоторое число M > 0 (Cij + M = 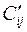 ), такое, что получим матрицу
), такое, что получим матрицу 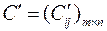 , для которой все
, для которой все 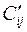 > 0. Игра с матрицей
> 0. Игра с матрицей 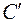 эквивалентна игре с матрицей C в том смысле, что оптимальные смешанные стратегии этих игр совпадают, а цена игр отличается на число M (во второй игре цена больше на M, чем в первой).
эквивалентна игре с матрицей C в том смысле, что оптимальные смешанные стратегии этих игр совпадают, а цена игр отличается на число M (во второй игре цена больше на M, чем в первой).
Рассмотрим игру двух лиц A и B с нулевой суммой. У игрока A – m чистых стратегий Ai, 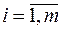 ; а у игрока B – n чистых стратегий Bj,
; а у игрока B – n чистых стратегий Bj, 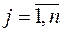 .
.
Платежная матрица имеет вид:
| Bj Ai | B 1 | B 2 | … | Bj | … | Bn |
| A 1 | C 11 | C 12 | … | C 1 j | … | C 1 n |
| A 2 | C 21 | C 22 | … | C 2 j | … | C 2 n |
| … | … | … | … | … | … | … |
| Ai | Ci 1 | Ci 2 | … | Cij | … | Cin |
| … | … | … | … | … | … | … |
| Am | Cm 1 | Cm 2 | … | Cmj | … | Cm n |
Пусть α ≠ β, седловой точки нет и смешанные стратегии игроков будем искать в виде.
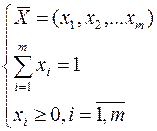
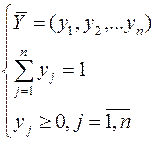
При любой стратегии Bj игрока B выигрыш игрока A должен быть не менее чем цена игры v, то есть:
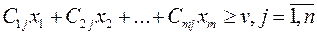 (1).
(1).
Разделим на v левую и правую части:
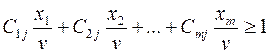 (2).
(2).
Обозначим 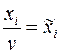 (3), тогда
(3), тогда 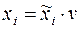 (4) и получим:
(4) и получим:
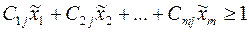 ,
, 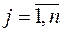 (5).
(5).
Подставим (4) в выражение 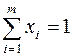 получим:
получим:
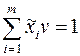 =>
=> 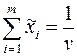 , и так как v → max, то
, и так как v → max, то 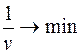 , отсюда получим целевую функцию:
, отсюда получим целевую функцию:
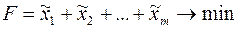 .
.
Математическая модель задачи игрока A имеет вид:
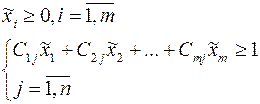
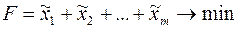
или
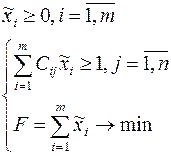 , где
, где 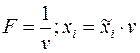 ,
, 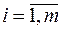 .
.
Рассуждая аналогично относительно действий игрока B, получим задачу игрока B:
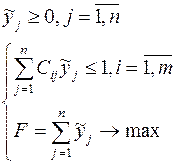 , где
, где 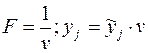 ,
, 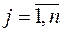 .
.
Решив пару двойственных задач линейного программирования, получим решение игры.
 2015-09-07
2015-09-07 454
454








