Дизъюнктивная нормальная форма

Булева формула (по имени Джорджа Буля) — формула логики высказываний. Может содержать логические переменные и пропозициональные связки — конъюнкцию (" 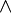"), дизъюнкцию (" 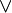"), отрицание (" ") и другие. Формула называется тождественно истинной (ложной), если она истинна (ложна) при любых значениях переменных. Две булевы формулы называются эквивалентными тогда и только тогда, когда они истинны на одном и том же подмножестве множества значений аргументов. Булева формула от n переменных определяет булеву функцию 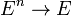. 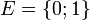- множество значений каждой переменной 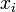, значение 0 соответствует тому, что 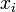ложно, а значение 1 соответствует тому, что 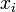истинно. Всего существует 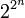булевых функций, поэтому существует столько же классов эквивалентных булевых формул.

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.