Графическое решение задачи приведено на рисунке 8.1

Ограничения здесь задают область допустимых решений в форме (заштрихованного) четырехугольника, а семейство (пунктирных) прямых, представляет собой линии уровня целевой функции F.

Существует два крайних положения линии уровня, когда она «касается» допустимого множества. Этим двум положениям в данном случае соответствуют две точки «касания» -начало координат (0, 0) и точка (9, 13). Первая из этих точек - точка минимума, а вторая - максимума данной функции F вида (1) на допустимом множестве (2).

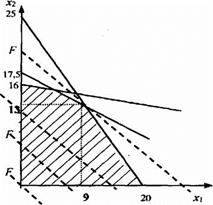
Рис. 8.1. Графическое решение ЗЛП

В случае большего числа разнородных ограничений графическая интерпретация задачи затруднена, поэтому задачу представляют в математической форме и используются специальные методы.

Постановка данной задачи выглядит следующим образом.

Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:

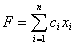(8.1)

Имеются ограничения, которые представляют собой линейные формы

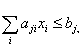где 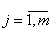. (8.2)

Задача линейного программирования формулируется так:

Определить максимум линейной формы

F(x1,…,xn)=max(c1x1+…+cnxn) (8.3)

при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств

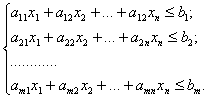(8.4)

Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств (8.4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство

c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn

для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования.

Задачу линейного программирования удобно представлять в векторной форме, тогда она будет выглядеть следующим образом: найти max F(x) = max (cTx) при условии АХ ≤Ро; Х≥0,

где с = (с1,с2,..., сn) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем сT-транспонированная вектор-строка; х = (х1, х2,..., хп) - п-мерный вектор переменных решений;

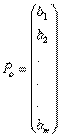- m-мерный вектор свободных членов ограничений;

Матрица А размером (m×n) - матрица, составленная из коэффициентов всех линейных ограничений:

Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.

Каноническая задача линейного программирования заключается в минимизации (максимизации) линейной целевой функции

F(x) = clx1+c2x2+... + cnxn при ограничениях

a11х1 +а12х2 +...+а1пхn=b1

а21х1 +а22х2 +...+а2пхn=b1…

…

аm1х1 +аm2х2 +...+аmпхn=b1

xt,x2,...,xn>0.

где с[,с2,...,сп - коэффициенты целевой функции, atJ, i = \, 2,...,n,j = 1, 2,...,m -коэффициенты системы ограничений, а b1,bг,...,bn - свободные члены, которые считаются неотрицательными.

Вектор X = (xi, х2,..., xj, удовлетворяющий ограничениям задачи ЛП, называется допустимым решением или планом. Допустимый план X* =(xl,x'2,...,x'n), при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, на­зывается оптимальным планом.

Иными словами, каноническая задача линейного программирования (ЛП) состоит в нахождении среди всех решений выписанной выше системы линейных уравнений такого ее неотрицательного решения, на котором достигает своего минимального (максимального) значения линейная целевая функция z от и переменных.

В задаче линейного программирования общего вида вместо некоторых (всех) равенств в ограничениях записаны нестрогие неравенства в ту или другую сторону; при этом усло­вие неотрицательности переменных может отсутствовать для части или же для всех переменных. Известно, что решение любой задачи линейного программирования может быть сведено к решению канонической задачи, представляемой в форме (1) или (4).

Линейное программирование (ЛП) первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций на выпуклом множестве (см. выпуклое программирование). Понятие целевой функции, удобное для приложений, сформировалось позднее.

Наиболее простым и распространенным методом решения канонической задачи линейного программирования до сих пор является симплекс-метод, предложенный в 40-е годы прошлого века Дж. Данцигом. Геометрически идею симплекс-метода в упрощенной форме можно выразить следующим образом. Допустимым множеством в задаче линейного программирования является некоторое многогранное множество и-мерного векторного пространства (в частном случае n = 2 - это выпуклый и не обязательно ограниченный многоугольник). Работа симплекс-метода начинается с некоторой начальной вершины (начального опорного плана) многогранного множества. Специальным образом выясняется, нет ли среди соседних вершин такой, в которой значение целевой функции лучше? Если такая вершина находится, то она и принимается за следующее приближение. После этого вновь исследуются соседние вершины для полученного приближения и т. д. до тех пор, пока не будет получена вершина, среди соседних вершин которой не существует вершины с лучшим значением целевой функции. Такая вершина является оптимальной. Она соответствует оптимальной точке (оптимальному решению) задачи линейного программирования.

В настоящее время разработан широкий круг различных численных методов решения задач линейного профаммирования, каждый из которых учитывает ту или иную специфическую особенность имеющейся задачи линейного профаммирования.

Кроме симплекс-метода имеются и другие методы решения специальных задач ЛП: метод потенциалов, Венгерский метод, двойственный симплекс-метод, метод обратной матрицы (модифицированный симплекс-метод) и др.

В настоящее время линейное профаммирование представляет собой область математики, посвященную разработке теории и численных методов решения экстремальных задач с линейными целевыми функциями и линейными ограничениями в виде систем равенств и/или неравенств. С применением линейного программирования решается широкий круг задач экономического характера: задачи о комплексном использовании сырья, рационального раскроя материалов, задачи загрузки оборудования, размещения заказов по однородным предприятиям, задачи о смесях, задачи текущего производственного планирования (статическая модель), задачи перспективного оптимального планирования, транспортная задача.

18. Симплекс метод

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Общую идею симплекс-метода можно проиллюстрировать на примере модели, посроенной для нашей задачи. Пространство решений этой задачи представим на рис. 1. Исходной точкой алгоритма является начало координат (точка А на рис. 1). Решение, соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке.