Критерий оптимизации

Критерий оптимизации — некий показатель, значение которого определяет качество тестируемого набора входных параметров. Чем больше значение критерия оптимизации, тем лучше оценивается результат тестирования с данным набором параметров. Выбор данного показателя осуществляется на вкладке "Настройки", справа от поля "Оптимизация".

Критерий оптимизации необходим только для генетического алгоритма.

Доступны следующие критерии оптимизации:

•Максимальный баланс — показателем оптимизированности является максимальное значение баланса;

•Баланс + максимальная прибыльность — показателем является максимальное значение произведения баланса наприбыльность;

•Баланс + максимальное матожидание выигрыша — показателем является произведение баланса на матожидание выигрыша;

•Баланс + минимальная просадка — в данном случае помимо значения баланса учитывается уровень просадки: (100% - Просадка)*Баланс;

•Баланс + максимальный фактор восстановления — показателем является произведение баланса на фактор восстановления;

•Баланс + максимальный коэффициент Шарпа — показателем является произведение баланса на коэффициент Шарпа;

•Пользовательский критерий оптимизации — при выборе данного параметра в качестве критерия оптимизации будет учитываться значение функции OnTester() в советнике. Данный параметр позволяет пользователю использовать любой собственный показатель для оптимизации.

Свертка критериев http://otherreferats.allbest.ru/emodel/00131580_0.html

В многокритериальных задачах, когда из первоначальной постановки не удается выделить критерий, преобладающий по важности над другими - главный критерий, довольно часто критерии искусственно комбинируют посредством агрегирующей функции, с параметрами - весовыми коэффициентами, назначаемыми каждому критерию согласно его относительной важности. Этот подход часто называют скаляризацией или сверткой векторного критерия. А получающуюся при этом параметризованную функцию, сводящую исходную многокритериальную задачу к однокритериальной, - обобщенным, агрегированным, глобальным критерием или суперкритерием. Наиболее широко распространенным видом обобщенного критерия является линейная свертка, когда глобальный критерий представляется в виде суммы (иногда произведения) частных критериев, умноженных на соответствующие весовые коэффициенты.

При применении этого способа определенные трудности вызывает правильный выбор весовых коэффициентов, проблематична интерпретация получаемых результатов. Использовать рассмотренный прием образования обобщенного критерия имеет смысл только в тех случаях, когда интерес представляет сумма отдельных критериальных функций. В общем же случае происходит просто замена одних неопределенностей другими, замаскированная математическими выкладками [2].

Существуют также случаи, когда довольно проблематично назначить каждому критерию определенный весовой коэффициент, соответствующий его важности относительно остальных. Тогда прибегают к свертке критериев где весовые коэффициенты не отражают относительной важности критериев, а изменяясь в определенных пределах, способствуют тем самым локализации точек в множестве Парето. При этом еще больше возрастает роль ЛПР, т.к. при выборе весовых коэффициентов он руководствуется в основном собственным опытом и интуицией, что также требует от него определенной квалификации.

Неоднократно отмечались ошибки и противоречия, которые делает человек при назначении весов критериев. Достаточно обстоятельный обзор различных методов назначения весов подводит к выводу, что не существует корректных методов решения человеком этой задачи. Такое поведение человека при решении многокритериальных зада является повторяющимся и устойчивым.

Имеются результаты экспериментов, из которых следует, что человек назначает веса критериев с существенными ошибками по сравнению с объективно известными, что назначаемые веса противоречат его непосредственным оценкам альтернатив и т.д. Хотя дискуссия о возможности использования весов в методах принятия решений еще продолжается, полученных данных уже достаточно, чтобы считать эту операцию достаточно сложной для ЛПР [4].

Суммируя сказанное можно сделать следующий вывод. Метод сверток применялся и применяется наиболее часто, но имеет труднопреодолимые недостатки [11, 17]:

- не всегда потеря качества по одному критерию компенсируется приращением по другому. «Оптимальное» по свертке решение может характеризоваться низким качеством некоторых частных критериев и в связи с этим будет неприемлемым;

- не всегда можно задать веса критериев. Зачастую известна лишь сопоставимая важность критериев, иногда нет никакой информации о важности;

- результат сильно зависит от предпочтений ЛПР, который чаще всего назначает веса, исходя из интуитивного представления о сравнительной важности критериев;

- величина функции цели, полученная по свертке, не имеет никакого физического смысла;

- многократный запуск алгоритма по свертке может давать только несколько различных точек Парето (или одну и ту же) даже в случае, когда в действительности этих точек очень много;

- данный подход не способен генерировать истинные Парето-оптимальные решения в условиях невыпуклых поисковых пространств, что является серьезным препятствием при решении многих практических задач.

Итак, для решения любой многокритериальной задачи необходимо учитывать сведения об относительной важности частных критериев.

В некоторых многокритериальных задачах частные критерии строго упорядочены по важности так, что следует добиваться приращения более важного критерия за счет любых потерь по всем остальным менее важным критериям. Но в большинстве случаев возникает ситуация, когда выделить главный или упорядочить критерии по важности не удается. Тогда зачастую прибегают к свертке критериев в обобщенный критерий. Применение данного подхода к формированию множества Парето, также как методов последовательных уступок и выделения основного частного критерия, связано с рядом возникающих при этом трудностей, что ставит вопрос о целесообразности использования подобных подходов и необходимости разработки методов, лишенных их недостатков.

К тому же, характерной чертой, объединяющей 3 рассмотренных подхода, является то, что в каждом из них задача многокритериальной оптимизации сводится к одной или нескольким задачам однокритериальной оптимизации.

Таким образом, теряется суть решаемой задачи, ее отличительная особенность - одновременный учет многих критериев. А сами методы должны работать многократно, чтобы сгенерировать множество точек Парето с тем, чтобы дальше выполнить оценку решения, значительно увеличивая затрачиваемые при этом вычислительные ресурсы.

17. Линейное программирование

Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x1, …, xn, доставляющие оптимум заданной линейной формы z=c1x1 + c2x2+… + cnxn при выполнении системы ограничений, представляющих собой также линейные формы.

Постановка задачи линейного программирования.

Родоначальником линейного программирования считают д-ра физ.-мат. наук, лауреата Государственной и Нобелевской премий Л.В. Канторовича, который в 30-е годы XX века предложил метод решения экономических задач (в частности, задачи раскроя фанеры). Л.В. Канторович разработал метод разрешающих множителей для решения задачи линейного программирования.

В последующем, в 50-е гг. XX в. независимо от Канторовича метод решения задачи линейного программирования (так называемый симплекс-метод) был развит американским математиком Дж. Данцигом, который в 1951 г. и ввел термин «линейное программирование».

Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными.

Приведем простейший пример задачи линейного программирования.

Предположим, что в трех цехах (Ц1, Ц2, ЦЗ) изготавливается два вида изделий И1 и И2. Известна загрузка каждого цеха аi (оцениваемая в данном случае в процентах) при изготовлении каждого из изделий и прибыль (или цена, объем реализуемой продукции в рублях) сi от реализации изделий. Требуется определить, сколько изделий каждого вида следует производить при возможно более полной загрузке цехов, чтобы получить за рассматриваемый плановый период максимальную прибыль или максимальный объем реализуемой продукции.

Такую ситуацию удобно отобразить в таблице, которая подсказывает характерную для задач математического программирования форму представления задачи, т. е. целевую функцию (в данном случае определяющую максимизацию прибыли или объема реализуемой продукции)

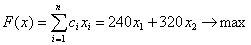(1)

и ряд ограничений (в данном случае диктуемых возможностями цехов, т.е. их предельной 100%-ной загрузкой)

5 х1 + 4х2 ≤ 100;

1.6 х1+ 17.4 х2 ≤ 100; (2)

2.9 х1 + 5.8 х2 ≤ 100.

Изделие	Цех (участок)	Цена
	Ц1	Ц2	ЦЗ	Изделия
И1	5%	1.6%	2.9%	240 руб.
И2	4%	17.4%	5.8%	320 руб.
Максимальная загрузка	100%	100%	100%

Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.