Теоремы Куна—Таккера

В предыдущем разделе построены условия Куна—Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна — Танкера тесно связаны с необходимыми условиями опти­мальности. В данном разделе рассматриваются строгие формули­ровки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования.

Теорема 1. Необходимость условий Куна—Таккера

Рассмотрим задачу нелинейного программирования (0)-(2). Пусть 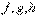- дифференцируемые функции, а х* — допус­тимое решение данной задачи. Положим 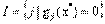. Далее пусть 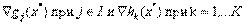линейно неза­висимы. Если х* — оптимальное решение задачи нелинейного про­граммирования, то существует такая пара векторов 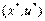, что 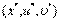является решением задачи Куна—Таккера (3)—(7).

Условие, согласно которому 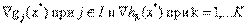должны быть линейно независимыми, известно как ус­ловие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое поч­ти всегда выполняется для встречающихся на практике задач опти­мизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свой­ствами.

1. Все ограничения в виде равенств и неравенств содержат линейные функции.

2. Все ограничения в виде неравенств содержат вогнутые функ­ции, все ограничения-равенства — линейные функции, а также существует, по крайней мере, одна допустимая точка х, которая рас­положена во внутренней части области, определяемой ограниче­ниями-неравенствами. Другими словами, существует такая точка х, что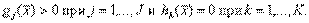

Если условие линейной независимости в точке оптимума не вы­полняется, то задача Куна—Таккера может не иметь решения.