Производная по направлению

(Производная Гато) Производной функционала 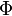в точке 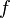по направлению 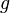, очевидно, будет

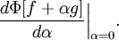
Этого в принципе уже достаточно для решения типичной вариационной задачи — нахождения «стационарных точек», то есть таких функций 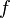, для которых первая вариация или производная по направлению обращается в ноль для любой бесконечно малой 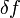или любой конечной 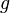. Именно эти «точки» в пространстве функций — то есть именно такие функции — являются кандидатами в экстремали (проверку того, действительно ли они являются экстремалями, то есть достигается ли на них локальный экстремум, надо делать отдельно, как и в случае функций конечномерного аргумента; интересно, что во многих задачах физики важнее найти не экстремали, а именно стационарные точки).