Для интегральных функционалов, которые являются очень важным для математики и приложений случаем, можно ввести не только аналог дифференциала и производную по направлению, но и производную Фреше — аналог конечномерного градиента, называемую вариационной производной.
То есть, в полной аналогии с конечномерным случаем, когда
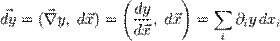 , где
, где 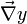 — обозначение градиента (или производной Фреше) функции
— обозначение градиента (или производной Фреше) функции 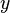 , а
, а 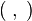 — скалярное произведение;
— скалярное произведение; 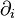 — оператор частной производной по
— оператор частной производной по 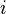 -той координате, сумма представляет собой полный дифференциал.
-той координате, сумма представляет собой полный дифференциал.
Для функционала имеем
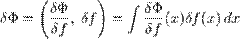 , где
, где 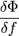 — обозначение вариационной производной
— обозначение вариационной производной 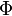 , а суммирование конечномерной формулы естественно заменено интегрированием.
, а суммирование конечномерной формулы естественно заменено интегрированием.
Итак, 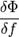 — стандартное обозначение вариационной производной. Это также некая функция как от
— стандартное обозначение вариационной производной. Это также некая функция как от 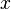 , так и
, так и 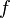 (вообще говоря, это обобщённая функция, но эта оговорка выходит за рамки рассмотрения, так как предполагается, что все функции и функционалы сколь угодно гладки и не имеют особенностей).
(вообще говоря, это обобщённая функция, но эта оговорка выходит за рамки рассмотрения, так как предполагается, что все функции и функционалы сколь угодно гладки и не имеют особенностей).
Иными словами, если можно представить вариацию
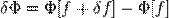
в виде
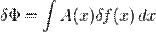 , где
, где 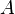 — некоторая функция
— некоторая функция 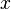 , то
, то 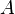 есть вариационная производная
есть вариационная производная 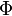 по
по 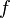 («по
(«по 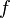 » здесь означает, что остальные аргументы или параметры не меняются; речевой оборот «по
» здесь означает, что остальные аргументы или параметры не меняются; речевой оборот «по 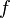 » можно опустить в случае, когда точно определено, функционалом от какой функции рассматривается
» можно опустить в случае, когда точно определено, функционалом от какой функции рассматривается 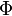 , что на практике может быть не ясным из самой его формулы, в которую могут входить и другие параметры и функции — см. также ниже). То есть
, что на практике может быть не ясным из самой его формулы, в которую могут входить и другие параметры и функции — см. также ниже). То есть
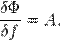
Легко видеть, что это определение обобщается на любую размерность интеграла. Для 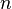 -мерного случая верна прямо обобщающая одномерный случай формула:
-мерного случая верна прямо обобщающая одномерный случай формула:
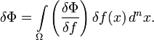
Так же легко обобщается понятие вариационной производной на случай функционалов от нескольких аргументов[4]:
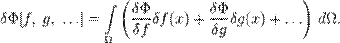
 2015-09-06
2015-09-06 1913
1913








