2015-09-06
311
При растяжении стержня постоянного поперечного сечения длина увеличивается, а поперечные размеры уменьшаются (рис. 13).
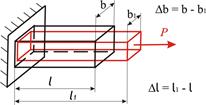
Рис. 13
Из закона Гука
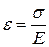
Учитывая то, что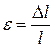 
и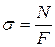 
имеем:
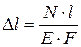
Если на рассматриваемом участке продольная сила и поперечное сечение переменны, то удлинение участка длиной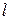 
получим, суммируя удлинения бесконечно малых участков.
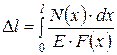
где 
- координата бесконечно малого участка;
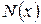- продольная сила в сечении с координатой ;
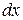- длина бесконечно малого участка;
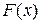- площадь поперечного сечения стержня с координатой .
Если мы возьмем произвольный поперечный размер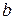 
, то его изменение, отнесенное к его первоначальному значению, даст нам относительную поперечную деформацию (рис. 13):
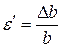
Между поперечной и продольной относительной деформацией при простом растяжении (сжатии) в пределах применимости закона Гука существует постоянное отношение. Абсолютная величина этого отношения носит название Коэффициента Пуассона и обозначается буквой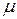 
:
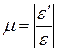
Учитывая, что продольная и поперечная деформация всегда имеют противоположные знаки, получаем
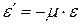
Коэффициент Пуассона наряду с модулем продольной упругости характеризует упругие свойства материалов.
В некоторых случаях для обеспечения нормальной работы конструкций размеры их элементов нужно выбирать так, чтобы обеспечивалось условие жесткости. При растяжении (сжатии) условие жесткости имеет следующий вид:
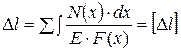
где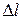 
- изменение размеров детали;
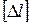- допускаемая величина этого изменения.
Расчет по условию жесткости всегда следует дополнять расчетом на прочность.
Список литературы
[1] Тимко И. А. Сопротивление материалов. Изд-во харьковского университета. 1970 г. 347 с.
[2] Сопротивление материалов/ Под ред. акад. АН УССР Писаренко Г. С. – 5-е изд., перераб. и доп. – К: Вища шк. Головное изд-во, 1986.- 775 с.
[3] Архипов О. Г., Кравцова Е. М., Галабурда Н. І. Механіка. Навч. посібник - Видавництво Східноукраїнського національного університету імені Володимира Даля. 2005.-252с.
[4] http://www.soprmat.kstu.ru/rast.htm
