2015-09-06
347
Если температура газа в разных местах различна, то будет различной и средняя кинетическая энергия его молекул. Перемещаясь вследствие теплового движения из одних мест в другие и сталкиваясь друг с другом, молекулы переносят запасенную ими энергию. Происходит процесс выравнивания средних кинетических энергий молекул в разных местах, т.е. выравнивание температур. В этом и заключается явление теплопроводности.
Перенос энергии в форме теплоты подчиняется закону Фурье:
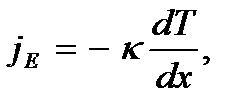
где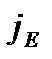 
– плотность потока тепла – величина, численно равная энергии, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси x; 
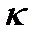– теплопроводность (коэффициент теплопроводности); 
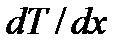– градиент температуры, равный скорости (быстроте) изменения температуры в направлении оси X. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры.
Расчет коэффициента теплопроводности можно провести аналогично расчету коэффициента диффузии. Следует только при этом заменить массу молекулы m на среднюю кинетическую энергию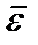 
и считать ее различной в слоях 1 и 2. Тогда для переносимой полной энергии через площадку 
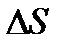за время 
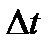будем иметь
=
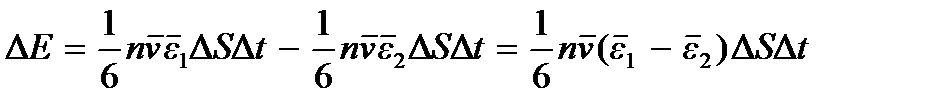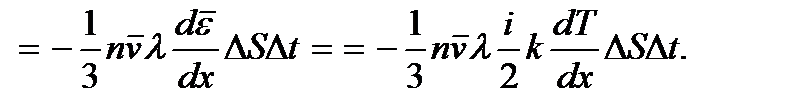
При получении конечного выражения было учтено, что средняя кинетическая энергия молекулы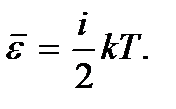 
Преобразуем выражение, стоящее перед градиентом температуры:
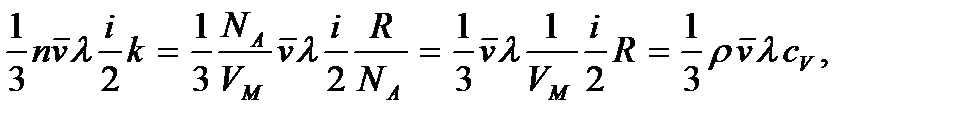
где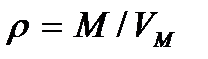 
– плотность газа, M – молярная масса газа, VM – молярный объем, 
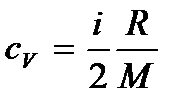– величина, называемая удельной теплоемкостью газа при постоянном объеме. С учетом этого получаем выражение для плотности потока энергии:
. 
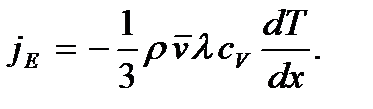
Мы пришли к формуле, выражающей закон Фурье. Следовательно, коэффициент теплопроводности
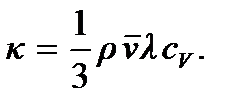
| (4.5) |
