Целью расчета является предотвращение остаточных деформаций или хрупкого разрушения поверхностного слоя или самих зубьев при действии максимального момента 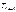 . Данный расчет выполняется при отсутствии в приводе предохранительных муфт, ременных передач и других устройств, защищающих привод от перегрузок. Действие максимальных нагрузок оценивают коэффициентом перегрузки
. Данный расчет выполняется при отсутствии в приводе предохранительных муфт, ременных передач и других устройств, защищающих привод от перегрузок. Действие максимальных нагрузок оценивают коэффициентом перегрузки 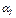 :
:
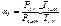 .
.
Для предотвращения остаточных деформаций или хрупкого разрушения поверхностного слоя максимальное расчетное контактное напряжение 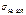 не должно превышать допускаемого напряжения [
не должно превышать допускаемого напряжения [ 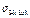 ]:
]:
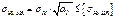 ,
,
где 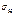 - расчетное контактное напряжение
- расчетное контактное напряжение
Допускаемое напряжение [ 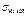 ] принимают при:
] принимают при:
- улучшении и сквозной закалке
[ 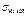 ]=
]= 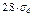 ;
;
- цементации или контурной закалке…
[ 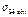 ]=
]= 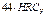 ;
;
-азотировании………………….
[ 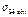 ]≈
]≈ 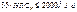 .
.
Для предотвращения остаточных деформаций и хрупкого разрушения зубьев максимальное расчетное напряжение изгиба 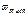 при действии пикового момента не должно превышать допускаемое
при действии пикового момента не должно превышать допускаемое
[ 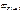 ]
]
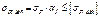
где 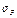 - расчетное напряжение изгиба, вычисленное при расчетах на сопротивление усталости.
- расчетное напряжение изгиба, вычисленное при расчетах на сопротивление усталости.
Проверку выполняют для зубьев шестерни и колеса в отдельности.
Допускаемое максимальное напряжение изгиба вычисляют в зависимости от вида термической обработки и возможной частоты приложения пиковой нагрузки:
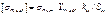 ,
,
где 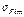 - предел выносливости при изгибе;
- предел выносливости при изгибе;
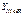 -максимально возможное значение коэффициента долговечности (
-максимально возможное значение коэффициента долговечности (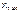 =4 - для сталей с объемной термообработкой: нормализация, улучшение, объемная закалка;
=4 - для сталей с объемной термообработкой: нормализация, улучшение, объемная закалка; 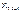 =2,5 – для сталей с поверхностной термообработкой: закалка ТВЧ, цементация, азотирование);
=2,5 – для сталей с поверхностной термообработкой: закалка ТВЧ, цементация, азотирование);
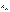 - коэффициент влияния частоты приложения пиковой нагрузки (в случае единичных перегрузок)
- коэффициент влияния частоты приложения пиковой нагрузки (в случае единичных перегрузок) 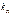 =1,2-1,3 – большие значения для объемной термообработки; при многократном (до 103)действии перегрузок
=1,2-1,3 – большие значения для объемной термообработки; при многократном (до 103)действии перегрузок 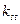 =1;
=1;
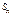 - коэффициент запаса прочности (обычно =2).
- коэффициент запаса прочности (обычно =2).
28)Червячная передача:
Достоинства: большое передаточное число, плавность, бесшумность работы, высокая кинематическая точность
Недостатки: низкий КПД, требует интенсивного охлаждения, сложность сборки и регулировки, необходимость использовать дорогие антифрикционные материалы.
Червяки по форме тела делят на:
1цилиндрические 2глобоидные 3тороидные
По форме боковой поверхности:
архимедовы (ZA) конвалютные (ZN) эвольвентные (Z1)с вогнутым профилем (ZT)
Геометрические параметры червяка и колеса
m – осевой модуль червяка
p = p×m – расчетный осевой шаг червяка
pX = p × z1 – ход витка (шаг винтовой линии)
g = arctg (pX / pd1) – делительный угол подъема линии витка
Делительный диаметр червяка:
d1 = m×z1 / tg g, причем z1 / tg g = q – коэффициент диаметра червяка.
d2 = mz2 – число зубьев колеса 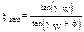
a = (d1 + d2) / 2 – межосевое расстояние
 2015-09-06
2015-09-06 478
478








