Односпрямовані списки

Найбільш простий динамічною структурою є односпрямований список, елементами якого служать об'єкти структурного типу (рис.).

Рисунок 21 – Лінійний односпрямований список

Опис найпростішого елемента такого списку виглядає таким чином:

struct імя_тіпа

{

інформаційне поле;

адресне поле;

};

• інформаційне поле - це поле будь-якого, раніше оголошеного або стандартного, типу;

• адресне поле - це покажчик на об'єкт того ж типу, що і визначувана структура, в нього записується адреса наступного елемента списку.

struct point

{

int data; / / інформаційне поле

point * next; / / адресне поле

};

Інформаційних полів може бути кілька.

Для того, щоб створити список, потрібно створити спочатку перший елемент списку, а потім у циклі додати до нього решту елементів. Додавання може виконуватися як на початок, так і в кінець списку.

/ / Створення односпрямованого списку

/ / Додавання в кінець

point * make_list (int n)

{

point * beg;/ / вказівник на перший елемент

point * p, * r;/ / допоміжні покажчики

beg = new (point);/ / виділяємо пам'ять під перший елемент

cout << "\ n?";

cin >> beg-> data;/ / вводимо значення інформаційного поля

beg-> next = 0;/ / обнуляем адресне поле

/ / Ставимо на цей елемент покажчик p (останній елемент)

p = beg;

for (int i = 0; i <n-1; i + +)

{

r = new (point);/ / створюємо новий елемент

cout << "\ n?";

cin >> r-> data;

r-> next = 0;

p-> next = r;/ / пов'язуємо p і r

/ / Ставимо на r покажчик p (останній елемент)

p = r;

}

return beg;/ / повертаємо beg як результат функції

}

Для обробки списку організується цикл, в якому потрібно переставляти покажчик p за допомогою оператора p = p-> next на наступний елемент списку до тих пір, поки вказівник p не стане дорівнює 0, тобто буде досягнутий кінець списку.

void print_list (point * beg)

/ / Друк списку

{

point * p = beg;/ / початок списку

while (p! = 0)

{

cout << p-> data << "\ t";

p = p-> next;/ / перехід до наступного елементу

}

}

В динамічні структури легко додавати елементи і з них легко видаляти елементи, тому що для цього достатньо змінити значення адресних полів.

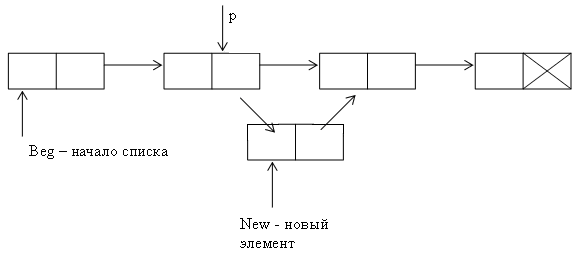
Рисунок 22 – Додавання елемента в список

point * add_point (point * beg, int k)

/ / додавання елемента з номером k

{

point * p = beg;/ / встали на перший елемент

point * New = new (point);/ / створили новий елемент

cout << "Key?"; cin >> New-> data;

if (k == 0) / / додавання в початок, якщо k = 0

{

New-> next = beg;

beg = New;

return beg;

}

for (int i = 0; i <k-1 && p! = 0; i + +)

p = p-> next;/ / проходимо по списку до (k-1) елемента або до кінця

if (p! = 0) / / якщо k-й елемент існує

{

New-> next = p-> next;/ / пов'язуємо New і k-й елемент

p-> next = New;/ ​​/ пов'язуємо (k-1) елемент і New

}

return beg;

}

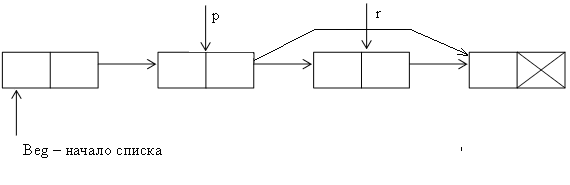
Рисунок 23 – Видалення елемента зі списку

point * del_point (point * beg, int k)

/ / Видалення елемента з номером k зі списку

{

point * p = beg;

if (k == 0) / / видалення першого елемента

{

beg = beg-> next;

delete p;

return beg;

}/ / Проходимо по списку до елемента з номером k-1

for (int i = 1; i <k&&p-> next! = 0; i + +)

p = p-> next;

/ * Якщо такого елемента в списку немає, то повертаємо покажчик на початок списку в якості результату функції * /if (p-> next == 0) return beg;

point * r = p-> next;/ / ставимо покажчик r на k-й елемент

p-> next = r-> next;/ / пов'язуємо k-1 і k +1 елемент

delete r;/ / видаляємо k-й елемент з пам'яті

return beg;

}

2.1. Двонаправлені списки

Двонаправлений список має два адресних поля, які вказують на наступний елемент списку і на попередній. Тому рухатися по такому списку можна як зліва направо, так і справа наліво.

/ / Формування двонаправленого списку

struct point

{

char * key;/ / адресне поле - динамічна рядок

point * next;/ / покажчик на наступний елемент

point * pred;/ / покажчик на попередній елемент

};

point * make_point ()

/ / Створення одного елемента

{

point * p = new (point);

p-> next = 0; p-> pred = 0;/ / обнуляем покажчики

char s [50];

cout << "\ nEnter string:";

cin >> s;

p-> key = new char [strlen (s) +1];/ / виділення пам'яті під рядок

strcpy (p-> key, s);

return p;

}

point * make_list (int n)

/ / Створення списку

{

point * p, * beg;

beg = make_point ();/ / створюємо перший елемент

for (int i = 1; i <n; i + +)

{

p = make_point ();/ / створюємо один елемент

/ / Додавання елемента в початок списку

p-> next = beg;/ / пов'язуємо р з першим елементом

beg-> pred = p;/ / пов'язуємо перший елемент з p

beg = p;/ / p стає першим елементом списку

}

return beg;

}

2.3. Черга і стек

Черга і стек - це окремі випадки односпрямованого списку.

У стеці додавання і видалення елементів здійснюються з одного кінця, який називається вершиною стека. Тому для стека можна визначити функції:

• top () - доступ до вершини стека

• pop () - видалення елемента з вершини;

• push () - додавання елемента в вершину.

Такий принцип обслуговування називають LIFO (last in - first out, останній прийшов, перший пішов).

У черзі додавання здійснюється в один кінець, а видалення з іншого кінця. Такий принцип обслуговування називають FIFO (first in - first out, перший прийшов, перший пішов). Для черзі також визначають функції:

• front () - доступ до першого елемента;

• back () - доступ до останнього елемента;

• pop () - видалення елемента з кінця;

• push () - додавання елемента в початок.

2.4. Бінарні дерева

Бінарне дерево - це динамічна структура даних, що складається з вузлів, каждий з яких містить, крім даних, не більше двох посилань на різні бінарні дерева. На кожен вузол є рівно одне посилання.

Описати таку структуру можна наступним чином:

struct point

{

int data;/ / інформаційне поле

point * left;/ / адресу лівого піддерева

point * right;/ / адресу правого піддерева

};

Початковий вузол називається коренем дерева. Вузол, що не має піддерев, називається листом. Вихідні вузли називаються предками, вхідні - нащадками. Висота дерева визначається кількістю рівнів, на яких розташовуватисьються його вузли.

Якщо дерево організовано таким чином, що для кожного вузла всі ключі його левого поддерева менше ключа цього вузла, а всі ключі його правого піддерева - більше, воно називається деревом пошуку. Однакові ключі не допускаються. У дереві пошуку можна знайти елемент по ключу, рухаючись від кореня і переходячи на ліве або праве піддерево в залежності від значення ключа в кожному вузлі. Такий пошук набагато ефективніше пошуку за списком, оскільки час пошуку визначається висотою дерева, а вона пропорційна двійковому логарифму количества вузлів.

В ідеально збалансованому дереві кількість вузлів справа і слева відрізняється не більше ніж на одиницю.

Лінійний список можна представити як вироджені бінарне дерево, в якому кожен вузол має не більше одного посилання. Для списку середній час пошуку одно половині довжини списку.

Дерева і списки є рекурсивними структурами, тому що кожне піддерево також є деревом. Таким чином, дерево можна визначити як рекурсивну структуру, в якій кожен елемент є:

• або порожній структурою;

• або елементом, з яким пов'язано кінцеве число піддерев.

Дії з рекурсивними структурами найзручніше описуються за допомогою рекурсивних алгоритмів.

2.4.1. обхід дерева

Для того, щоб виконати певну операцію над усіма вузлами дерева, всі вузли треба обійти. Така задача називається обходом дерева. При обході вузли повинні відвідуватися в певному порядку. Існують три принципи упорядкування. Розглянемо дерево, представлене на рис.

Корень

Левое поддерево

Правое поддерево

Рисунок 24 – Бінарне дерево

На цьому дереві можна визначити три методи упорядкування:

Зліва направо: Ліве піддерево - Корінь - Праве піддерево;

Зверху вниз: Корінь - Ліве піддерево - Праве піддерево;