а) Прямий оборотний цикл Карно. Як приклад колового процесу розглянемо цикл С.Карно, що зіграв величезну роль у розвитку термодинаміки і теплотехніки, оскільки дозволив підійти до аналізу коефіцієнтів корисної дії теплових машин. Схема роботи ідеальної теплової машини, що працює за циклом Карно, представлена на рис. 3.2:
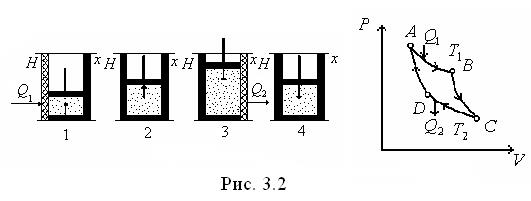
1. Від нагрівача 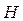 надходить теплота
надходить теплота 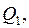 газ під поршнем за
газ під поршнем за 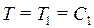 розширюється (ізотерма
розширюється (ізотерма 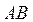 ). Оскільки процес рівноважний, то температура газу дорівнює температурі нагрівача.
). Оскільки процес рівноважний, то температура газу дорівнює температурі нагрівача.
2. Газ теплоізольований й адіабатно розширюється (адіабата 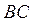 ), охолоджуючись до температури
), охолоджуючись до температури 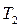 , що дорівнює температурі холодильника.
, що дорівнює температурі холодильника.
3. Газ ізотермічно 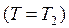 стискається (ізотерма СD), віддаючи холодильнику теплоту
стискається (ізотерма СD), віддаючи холодильнику теплоту 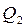 .
.
4. Газ адіабатно стискається (адіабата DА), нагріваючись до температури нагрівача 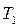 .
.
Знайдемо роботу, виконану ідеальним газом у даному циклі. Оскільки цикл коловий, то повна зміна внутрішньої енергії газу 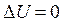 , а рівняння першого закону термодинаміки для робочого тіла (газу) у циклі Карно має вигляд:
, а рівняння першого закону термодинаміки для робочого тіла (газу) у циклі Карно має вигляд:
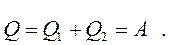 (3.1)
(3.1)
При цьому варто пам'ятати, що 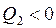 . Роботу циклу можна виразити як суму робіт окремих процесів циклу:
. Роботу циклу можна виразити як суму робіт окремих процесів циклу: 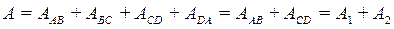 , оскільки сумарна робота адіабатного розширення й стиснення газу в даному циклі згідно з рівнянням (2.33) дорівнює нулю. На основі рівняння (2.25) знаходимо корисну роботу всієї маси газу
, оскільки сумарна робота адіабатного розширення й стиснення газу в даному циклі згідно з рівнянням (2.33) дорівнює нулю. На основі рівняння (2.25) знаходимо корисну роботу всієї маси газу 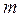 у даному циклі:
у даному циклі:
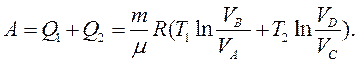 | |||
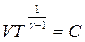 |
На основі рівняння адіабати отримаємо:
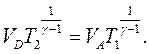
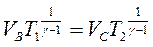
і
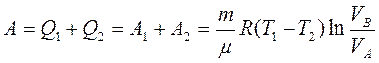 Врахувавши це, знаходимо:
Врахувавши це, знаходимо: 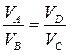 . Тоді корисна робота циклу буде дорівнювати: (3.2)
. Тоді корисна робота циклу буде дорівнювати: (3.2)
Оскільки 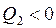 , то з рівняння (3.2) випливає, що ця робота менша від витраченої роботи
, то з рівняння (3.2) випливає, що ця робота менша від витраченої роботи 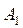 (і менша від наданої теплоти
(і менша від наданої теплоти 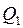 від нагрівача). Частина енергії віддається холодильнику у вигляді теплоти
від нагрівача). Частина енергії віддається холодильнику у вигляді теплоти 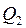 . Цей висновок справедливий для будь-якого колового процесу.
. Цей висновок справедливий для будь-якого колового процесу.
Величину 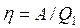 називають термічним коефіцієнтом корисної дії теплового двигуна. Для оборотного циклу Карно він дорівнює:
називають термічним коефіцієнтом корисної дії теплового двигуна. Для оборотного циклу Карно він дорівнює:
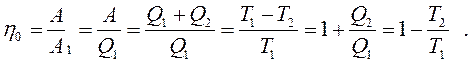 |
(3.3)
Формула (3.3) не містить ніяких даних про властивості робочого тіла та конструкції теплової машини. Отже, звідси випливає, що коефіцієнт корисної дії всіх оборотних машин, працюючих в ідентичних умовах, тобто за однієї і тієї самої температури нагрівача 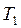 і одній і тій же температурі холодильника
і одній і тій же температурі холодильника 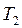 , однаковий і визначається тільки температурами нагрівача й холодильника. Це твердження називають теоремою Карно.
, однаковий і визначається тільки температурами нагрівача й холодильника. Це твердження називають теоремою Карно.
Теорема Карно служить підставою для встановлення так званої термодинамічної шкали температури. З рівняння (3.3) випливає, що 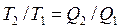 . Таким чином, для порівняння температур двох тіл
. Таким чином, для порівняння температур двох тіл 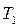 і
і 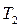 потрібно здійснити оборотний цикл Карно, у якому ці тіла використовуються як нагрівач і холодильник та порівняти теплоти
потрібно здійснити оборотний цикл Карно, у якому ці тіла використовуються як нагрівач і холодильник та порівняти теплоти  і
і  . Термодинамічна шкала не пов'язана із властивостями термодинамічного тіла. У цьому її перевага. Однак внаслідок необоротності реальних термодинамічних процесів такий спосіб порівняння температур практично нездійсненний і має лише принципове значення.
. Термодинамічна шкала не пов'язана із властивостями термодинамічного тіла. У цьому її перевага. Однак внаслідок необоротності реальних термодинамічних процесів такий спосіб порівняння температур практично нездійсненний і має лише принципове значення.
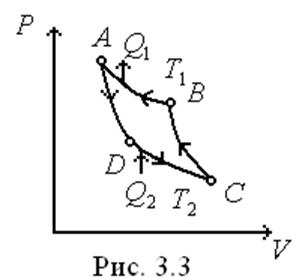 б) Зворотний рівноважний цикл Карно. У зворотному циклі Карно теплота
б) Зворотний рівноважний цикл Карно. У зворотному циклі Карно теплота 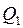 відводиться від газу в процесі ізотермічного стискання за температури
відводиться від газу в процесі ізотермічного стискання за температури 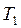 (рис 3.3), а теплота
(рис 3.3), а теплота 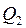 підводиться до газу в процесі ізотермічного розширення за температури
підводиться до газу в процесі ізотермічного розширення за температури 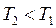 . Отже, в цьому випадку
. Отже, в цьому випадку 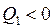 ,
, 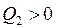 і сумарна робота
і сумарна робота 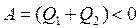 виконується зовнішнім середовищем над газом. Цей результат справедливий для будь-якого зворотного циклу. Таким чином, за рахунок здійснення роботи зовнішніми силами над робочим тілом можна переносити енергію у формі теплоти від менш нагрітого тіла до більш нагрітого.
виконується зовнішнім середовищем над газом. Цей результат справедливий для будь-якого зворотного циклу. Таким чином, за рахунок здійснення роботи зовнішніми силами над робочим тілом можна переносити енергію у формі теплоти від менш нагрітого тіла до більш нагрітого.
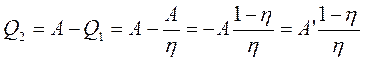 Цей метод широко застосовується в холодильній техніці. Холодильна техніка буде тим економнішою, чим менша робота
Цей метод широко застосовується в холодильній техніці. Холодильна техніка буде тим економнішою, чим менша робота 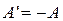 , затрачувана зовні на відведення від холодного тіла теплоти
, затрачувана зовні на відведення від холодного тіла теплоти 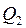 . З рівнянь
. З рівнянь 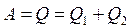 і
і 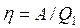 знаходимо:
знаходимо:
, (3.4)
де 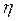 – термічний коефіцієнт корисної дії точно такого самого прямого циклу.
– термічний коефіцієнт корисної дії точно такого самого прямого циклу.
в) Необоротний цикл Карно. Нехай необоротність циклу зумовлена тим, що теплообмін між робочим тілом і нагрівачем і холодильником відбувається за кінцевих різниць температур: нагрівача й робочого тіла 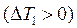 і робочого тіла й холодильника
і робочого тіла й холодильника 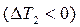 . Необоротний цикл неможливо характеризувати в будь-який момент часу заданими параметрами. Однак можна відповідним чином змінити параметри системи, і тоді розглядати необоротний цикл подібно оборотному. Так, при швидкому розширенні газу, що контактує з нагрівачем, його температура в середньому буде нижчою від температури нагрівача, а у разі швидкого стискання газу, що контактує з холодильником, температура газу в середньому буде вищою від температури холодильника. Отже, при визначенні коефіцієнта корисної дії необоротного циклу Карно температуру
. Необоротний цикл неможливо характеризувати в будь-який момент часу заданими параметрами. Однак можна відповідним чином змінити параметри системи, і тоді розглядати необоротний цикл подібно оборотному. Так, при швидкому розширенні газу, що контактує з нагрівачем, його температура в середньому буде нижчою від температури нагрівача, а у разі швидкого стискання газу, що контактує з холодильником, температура газу в середньому буде вищою від температури холодильника. Отже, при визначенні коефіцієнта корисної дії необоротного циклу Карно температуру 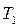 потрібно замінити на
потрібно замінити на 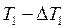 , а
, а 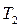 –– на
–– на 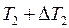 :
:
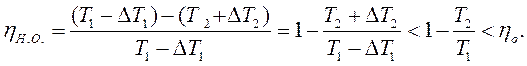 (3.5)
(3.5)
Можна показати, що термічний ККД будь-якого необоротного процесу завжди менший ніж ККД оборотного циклу Карно:
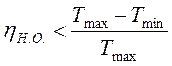 |
, (3.6)
де 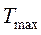 і
і 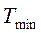 – екстремальні значення температур нагрівача й холодильника, які одержали загальну назву „джерел теплоти”.
– екстремальні значення температур нагрівача й холодильника, які одержали загальну назву „джерел теплоти”.
 2015-09-06
2015-09-06 771
771








