Ентропія і її властивості

Відношення теплоти 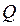, отриманої тілом в ізотермічному процесі, до температури 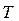„джерела теплоти” німецький Фізик Р. Клаузіус назвав зведеною кількістю теплоти :

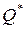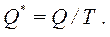(3.8)

При нагріванні тіла 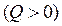зведена теплота 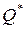позитивна, при охолодженні – негативна. Зведена кількість теплоти, надана тілу на кожній нескінченно малій ділянці процесу, дорівнює 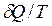. Сумуючи ці величини для всіх ділянок довільного ізотермічного процесу 1-2, одержимо таке вираження зведеної кількості теплоти:

^.

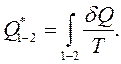Підрахуємо зведену кількість теплоти 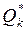, надану тілу в прямому оборотному циклі Карно (рис. 3.2):

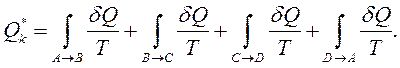В адіабатних процесах 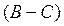і 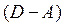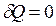.Тому:

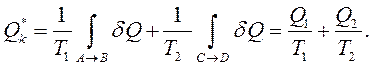
Відповідно до рівняння (3.7) для оборотного циклу Карно одержуємо:

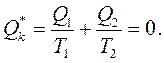(3.10)

Виявилося, що цей результат справедливий для будь-якого оборотного циклу. Його можна сформулювати в такий спосіб: „Зведена кількість теплоти, надана тілу в будь-якому оборотному коловому процесі, дорівнює нулю”:

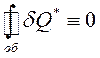. (3.11)

З тотожності (3.11) випливає, що підінтегральний вираз 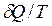, на відміну від 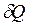, є повним диференціалом деякої функції :

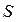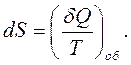(3.12)

Введену в такий спосіб у 1865 році Р. Клаузіусом функцію 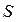називають ентропією. Подібно до внутрішньої енергії 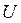, ентропія 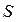є однозначною функцією стану системи. З рівняння (3.12) випливає, що 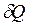та 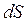мають один і той самий знак. Отже, за характером зміни ентропії системи можна судити про напрямок процесу теплообміну (при нагріванні тіла його ентропія зростає, при охолодженні – зменшується).

Як приклад розглянемо ентропію ідеального газу, для якого за першим законом термодинаміки з урахуванням рівняння (2.24) маємо:

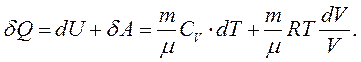Звідси знаходимо:

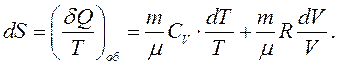(3.13)

Під час переходу ідеального газу зі стану 1 у стан 2 зміна його ентропії дорівнює:

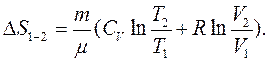(3.14)

З рівняння (3.14) випливає, що зміна ентропії ідеального газу не залежить від виду процесу, що є характерним для функції стану системи.

Ентропія системи тіл дорівнює сумі ентропії всіх тіл, що входять у систему. Розглянемо замкнену систему, що складається з нагрівача, холодильника, робочого тіла й споживача роботи. Зміна ентропії цієї системи під час здійснення робочим тілом циклу Карно дорівнює:

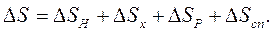Робоче тіло в результаті здійснення циклу Карно повертається у вихідний стан, тож зміна його ентропії 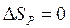. Споживач роботи одержує енергію тільки у формі роботи, і зміна його ентропії 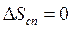. Зміна ентропії нагрівача й холодильника в ізотермічних процесах дорівнює:

;

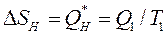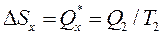Зміна ентропії розглянутої системи дорівнює:

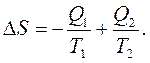(3.15)

Відповідно до нерівності Клаузіуса, у якій 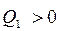, а 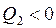, знаходимо:

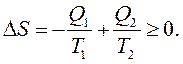(3.16)

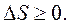В термодинаміці доведено, що отриманий висновок можна узагальнити на довільний процес, що відбувається в замкненій системі:

(3.17)

Словесне формулювання цього твердження може бути таким: „Ентропія замкненої системи за будь-яких протікаючих у ній процесів не може зменшуватись. У випадку оборотних процесів вона залишається незмінною 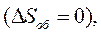у випадку необоротних – зростає ”.

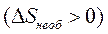З визначення ентропії 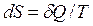випливає, що для оборотних процесів 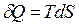, для необоротних:

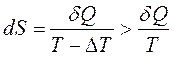
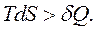і

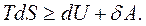З урахуванням цього рівняння першого закону термодинаміки можна записати у вигляді:

(3.18)