Внаслідок дії сил поверхневого натягу викривлений поверхневий шар чинить на рідину тиск 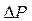 , в додаток до зовнішнього тиску
, в додаток до зовнішнього тиску 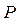 .
.
Знайдемо формулу для обчислення тиску 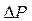 для найпростішого випадку, коли меніск має форму циліндричної поверхні з постійним радіусом кривизни
для найпростішого випадку, коли меніск має форму циліндричної поверхні з постійним радіусом кривизни 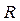 . Розглянемо нескінченно малий елемент поверхневого шару ABCD (рис 9.6, а). Тут показані сили, що діють на елемент ABCD з боку всієї іншої частини поверхневого шару. При цьому
. Розглянемо нескінченно малий елемент поверхневого шару ABCD (рис 9.6, а). Тут показані сили, що діють на елемент ABCD з боку всієї іншої частини поверхневого шару. При цьому 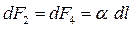 і
і 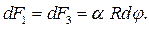 . Очевидно, що рівнодійна сил
. Очевидно, що рівнодійна сил 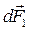 і
і 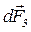 дорівнює нулю. Сила
дорівнює нулю. Сила 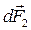 спрямована перпендикулярно до площини, охопленої контуром АОО΄В, сила
спрямована перпендикулярно до площини, охопленої контуром АОО΄В, сила 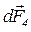 – перпендикулярно до площини, охопленої контуром DОО΄С.
– перпендикулярно до площини, охопленої контуром DОО΄С.
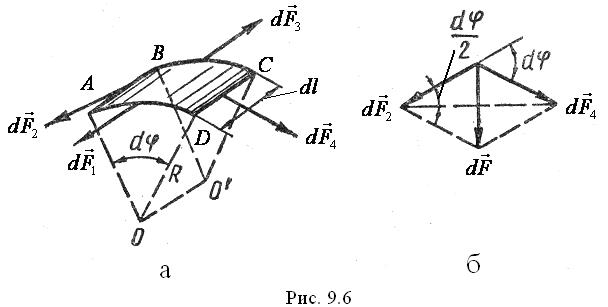
Очевидно, що кут між цими силами дорівнює 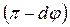 , а їх рівнодійна
, а їх рівнодійна 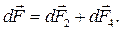 . З рис 9.6. б) видно, що:
. З рис 9.6. б) видно, що:
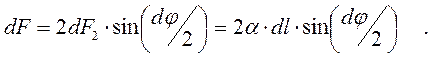 |
Оскільки за малих кутів 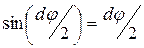 , то:
, то:
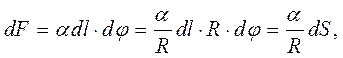 (9.15)
(9.15)
де 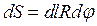 – площа поверхні ABCD. Ця сила спрямована до осі кривизни
– площа поверхні ABCD. Ця сила спрямована до осі кривизни 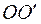 . Вона і спричиняє появу додаткового тиску
. Вона і спричиняє появу додаткового тиску 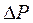 :
:
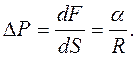 (9.16)
(9.16)
П. Лаплас довів, що додатковий тиск на рідину поверхневого шару довільної форми:
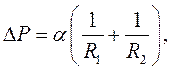 (9.17)
(9.17)
де 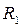 та
та 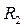 – радіуси кривизни двох взаємоперпендикулярних перерізів
– радіуси кривизни двох взаємоперпендикулярних перерізів 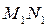 та
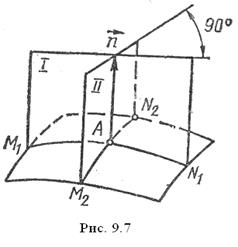
та 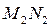 поверхні у вибраній точці А (рис 9.7).
поверхні у вибраній точці А (рис 9.7).
У формулі (9.17) радіус кривизни 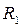 та
та 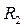 вважаються позитивними, якщо центр кривизни розташовані у рідині. У протилежному разі радіус кривизни перерізу вважається негативним. Отже, додатковий тиск
вважаються позитивними, якщо центр кривизни розташовані у рідині. У протилежному разі радіус кривизни перерізу вважається негативним. Отже, додатковий тиск 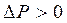 , якщо меніск опуклий, і
, якщо меніск опуклий, і 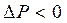 , якщо меніск ввігнутий.
, якщо меніск ввігнутий.
Формула (9.16) є окремим випадком формули (9.17), оскільки 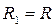 , а
, а 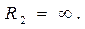
У випадку плоскої поверхні 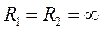 , і додатковий тиск
, і додатковий тиск 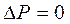 .
.
У випадку сферичної поверхні 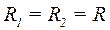 , і
, і
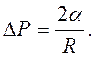 (9.18)
(9.18)
Такий надлишковий тиск всередині бульбашки газу радіуса 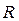 , що міститься у рідині біля її поверхні. Надлишковий тиск всередині мильної бульбашки такого самого радіуса вдвічі більший, оскільки він утворюється двома поверхневими шарами тонкої сферичної мильної плівки:
, що міститься у рідині біля її поверхні. Надлишковий тиск всередині мильної бульбашки такого самого радіуса вдвічі більший, оскільки він утворюється двома поверхневими шарами тонкої сферичної мильної плівки:
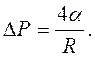 (9.19)
(9.19)
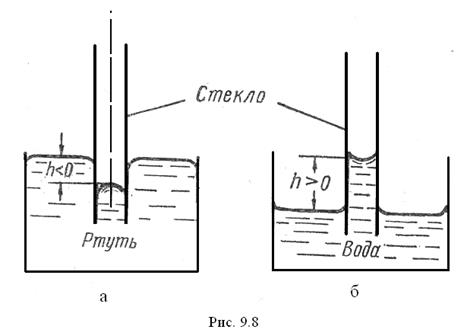
Рівень рідини у вузьких посудинах (капілярах) відрізняється від рівня рідини в сполученій з ними широкій посудині. Рівень рідини в капілярі нижчий, ніж в посудині (рис 9.8, а), якщо рідина не змочує стінок капіляра. Він вищий, ніж у посудині, якщо рідина змочує стінки капіляра (рис 9.8. б). Ці явища зумовлені великою кривизною меніска рідини в капілярі, а отже, значною величиною надлишкового тиску. Їх називають капілярними.
У широкій посудині поверхня рідини практично плоска, і додатковий тиск дорівнює нулю. Тому різниця між рівнями рідини в капілярі і широкій посудині залежить тільки від тиску 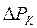 . Сума тиску
. Сума тиску 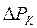 і гідростатичного тиску стовпчика рідини висотою
і гідростатичного тиску стовпчика рідини висотою 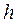 повинна дорівнювати нулю:
повинна дорівнювати нулю:
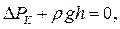
де 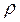 – густина рідини.
– густина рідини.
Таким чином, висота стовпчика рідини в капілярах:
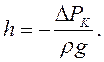
|
 Якщо капіляр являє собою круглу циліндричну трубку з радіусом канала
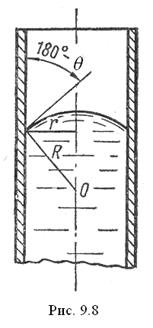
Якщо капіляр являє собою круглу циліндричну трубку з радіусом канала 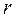 , то меніск має сферичну форму.
, то меніск має сферичну форму.
Як видно з (рис 9.9), радіус меніска:
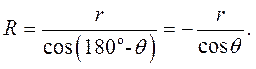
Додатковий тиск 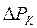 і висота
і висота 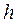 підйому рідини в круглому капілярі відповідно дорівнюють:
підйому рідини в круглому капілярі відповідно дорівнюють:
|
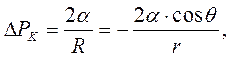
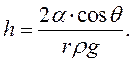
Якщо капіляр має форму вузької щілини з постійною шириною 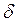 , то меніск має циліндричну форму з радіусом:
, то меніск має циліндричну форму з радіусом:

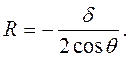
Відповідно:
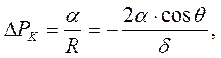
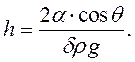
Капілярні явища відіграють важливу роль в природі і техніці. Наприклад, обмін вологою в грунті відбувається за рахунок підняття води тоненькими капілярами. Під час переорювання грунту капіляри порушуються, що сприяє збереженню вологи у грунті.
На явищі змочування рідиною одних твердих речовин і незмочування інших засновано флотаційний метод збагачення руди. Принцип флотації полягає в такому. Подрібнену руду, котра складається з частинок руди і некорисних домішок (“пустої” породи) змішують з рідиною, що змочує лише частинки “пустої” породи. Через цю суміш пропускають повітря. Бульбашки повітря “прилипають” до незмочених рідиною частинок руди і підіймають їх на поверхню. Частинки “пустої” породи, до яких не прилипають бульбашки повітря, поступово осідають на дно.
Захист металевих поверхонь від корозії за допомогою масляних плівок заснований на незмочуванні водою жирних поверхонь.
Існує ряд експериментальних методів визначення коефіцієнта поверхневого натягу. З одним із них – методом Стокса – студенти ознайомлюються на лабораторних заняттях.
 2015-09-06
2015-09-06 940
940








