Пусть имеется m инвесторов, владеющих инвестициями в количествах 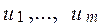 . Инвесторы могут использовать свои инвестиции в n инвестиционных проектах с потребностями инвестиций в объемах
. Инвесторы могут использовать свои инвестиции в n инвестиционных проектах с потребностями инвестиций в объемах 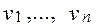 . Известны нормативные коэффициенты эффективности
. Известны нормативные коэффициенты эффективности 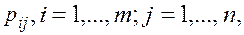 использования единицы инвестиций
использования единицы инвестиций 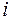 -го инвестора в
-го инвестора в 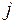 - м проекте. Требуется определить инвестиционные потоки
- м проекте. Требуется определить инвестиционные потоки 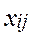 , направляемые от
, направляемые от 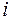 -го инвестора к
-го инвестора к 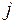 -ому инвестиционному проекту таким образом, чтобы получить максимальную эффективность от инвестирования.
-ому инвестиционному проекту таким образом, чтобы получить максимальную эффективность от инвестирования.
Аналогично, возможны случаи:
Возможны случаи:
а) 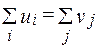 - общее количество инвестиций равно суммарному объему требуемых для инвестиций средств
- общее количество инвестиций равно суммарному объему требуемых для инвестиций средств
б) 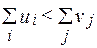
в) 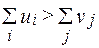
Если имеет место случай б), то вводится фиктивный инвестор 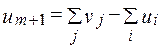
Если имеет место случай в), то вводится фиктивный проект с объемом средств 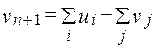
При этом нормативные коэффициенты эффективности полагают равными нулю.
Рассмотрим числовой пример задачи инвестиционного управления.
Дано: m =3, n =4,
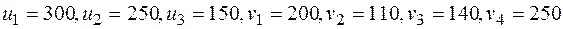 ;
;
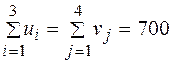 , т.е. имеем закрытую модель.
, т.е. имеем закрытую модель.
Пусть матрица нормативных коэффициентов эффективности имеет вид:
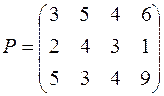
Взаимосвязь инвесторов и проектов удобно представлять, как и в транспортных задачах, в виде таблицы (табл. 5).
Таблица 5
Схема инвестиционных потоков
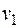 =200
=200 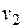 =110
=110 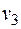 =140
=140 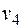 =250
=250
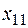 3 3 | 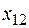 5 5 | 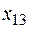 4 4 | 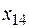 6 6 |
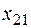 2 2 | 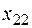 4 4 | 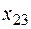 3 3 | 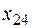 1 1 |
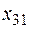 5 5 | 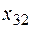 3 3 | 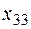 4 4 | 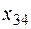 9 9 |
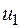 =300
=300
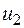 =250
=250
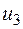 =150
=150
Размерность задачи: 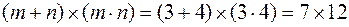
Требуется найти
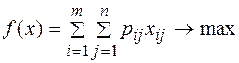
Или
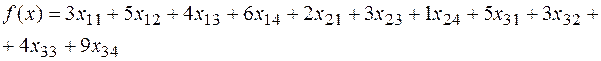
при ограничениях (в координатной форме):
 ≥0, i= 1,2,3; j =1,2,3,4
≥0, i= 1,2,3; j =1,2,3,4
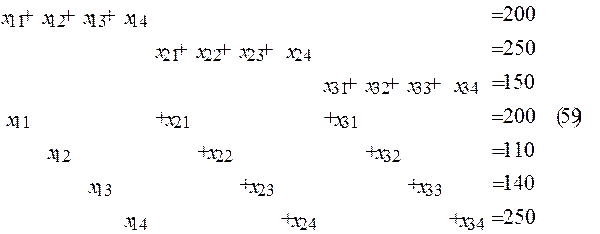
Запишем (59) в матричной форме. По теореме 7 одну строку, например, первую убираем и получаем систему линейно-независимых уравнений размерности 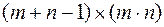 =
= 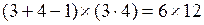 :
:

Рассмотрим модифицированный метод потенциалов для решения данной задачи.
Алгоритм поиска оптимального инвестиционного потока
1. Нахождение исходного допустимого базисного решения с помощью метода северо-западного угла, вычисляется значение целевой функции.
2. Вычисление оценок  свободных клеток (см. табл. 4),
свободных клеток (см. табл. 4),
при этом нужно перейти к другому базисному решению.
3. Вычисление для полученного решения целевой
функции (значение целевой функции должно улучшаться).
4. Шаги 3, 4 продолжаются до тех пор, пока не
получится оптимальное решение, т.е. все оценки свободных клеток  должны быть неположительными, т.е.
должны быть неположительными, т.е. 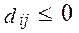 . При этом f (х)будет принимать максимальное значение. Если все
. При этом f (х)будет принимать максимальное значение. Если все 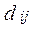 < 0, то решение единственное, если есть
< 0, то решение единственное, если есть 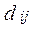 = 0, то решение может быть неединственным, так как на текущей итерации имеется возможность перехода к другому базису, не меняя значение целевой функции.
= 0, то решение может быть неединственным, так как на текущей итерации имеется возможность перехода к другому базису, не меняя значение целевой функции.
С помощью метода северо-западного угла найдем исходное допустимое решение, учитывая, что полностью используются инвестиционные возможности инвесторов и полностью удовлетворяются потребности проектов в инвестициях:
 300 300 | _ | _ | ||
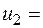 250 250 | _ | |||
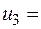 150 150 | _ | _ | _ | |
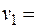 200 200 | 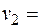 110 110 | 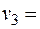 140 140 | 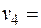 250 250 |
Итак, компоненты исходного допустимого базисного решения имеют вид:
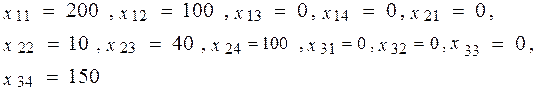
При этом количество ненулевых компонент или базисных решений (занятых клеток) 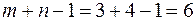 . Рассмотрим на данном примере, как осуществляется переход к другому базисному решению.
. Рассмотрим на данном примере, как осуществляется переход к другому базисному решению.
1. Для перехода к другому базисному решению одну свободную клетку (небазисную переменную) нужно сделать занятой (базисной), а одну занятую (базисную) – свободной (небазисной). Обозначим такую переменную через 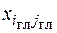 . Это означает, что переменная
. Это означает, что переменная 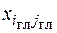 на текущей итерации была небазисной
на текущей итерации была небазисной 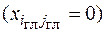 , в конце этой итерации становится базисной и примет значение в виде
, в конце этой итерации становится базисной и примет значение в виде 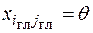 , где
, где 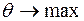 , а одна занятая клетка становится свободной. При этом новые базисные переменные должны удовлетворять всем ограничениям задачи.
, а одна занятая клетка становится свободной. При этом новые базисные переменные должны удовлетворять всем ограничениям задачи.
2. Перераспределение инвестиций будет зависеть от неотрицательного параметра 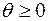 .
.
3. Для определения количества единиц инвестиций, подлежащих перераспределению, отмечаем знаком «+» незанятую клетку, в которую надо перераспределить инвестиции. Незанятая клетка присоединяется к занятым клеткам. В таблице занятых клеток стало т + п =7, поэтому появляется цикл, все вершины которого за исключением клетки, отмеченной знаком «+», находятся в занятых клетках:
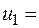 300 300 | _ + | _ | ||
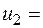 250 250 | _ | |||
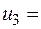 150 150 | _ | _ | _ | |
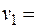 200 200 | 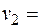 110 110 | 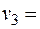 140 140 | 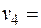 250 250 |
4. Отыскиваем цикл и, начиная движение от клетки «+», поочередно проставляем знаки «+» и «–».
Правило построения цикла:
· Цикл начинается с данной свободной клетки.
· Направление движения в цикле может быть как по часовой стрелке, так и против нее.
· Поворот на 90° происходит только в занятых клетках, т.е. вершины цикла находятся в занятых клетках.
· Стороны цикла могут проходить мимо некоторых занятых клеток и могут пересекаться. При текущем базисном решении каждой свободной клетке соответствует только один цикл.
· Цикл, построенный по приведенным выше правилам, позволяет выразить каждую базисную переменную через небазисную. В связи с этим, для каждой небазисной переменной существует только единственный цикл (см. теорему 6):
  _ _ | – 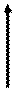 + + | _ | ||
| _ |  + + | – | ||
| _ | _ | _ | ||
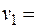 200 200 | 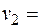 110 110 | 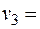 140 140 | 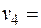 250 250 |
5. Находим  =min
=min 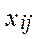 , где
, где 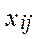 - инвестиции, стоящие в вершинах цикла, отмеченных знаком «–».
- инвестиции, стоящие в вершинах цикла, отмеченных знаком «–».
Свойства величины  :
:
· Величина  определяет, сколько единиц инвестиций можно перераспределить по найденному циклу.
определяет, сколько единиц инвестиций можно перераспределить по найденному циклу.
· Значение  записываем в незанятую клетку, отмеченную знаком «+», двигаясь по циклу, вычитаем
записываем в незанятую клетку, отмеченную знаком «+», двигаясь по циклу, вычитаем  из объемов инвестиций, расположенных в клетках, которые отмечены знаком «–» и прибавляем к объемам инвестиций, находящихся в клетках«+».
из объемов инвестиций, расположенных в клетках, которые отмечены знаком «–» и прибавляем к объемам инвестиций, находящихся в клетках«+».
· Если  соответствуют несколько минимальных инвестиций, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном решении занятых клеток было m+n- 1.
соответствуют несколько минимальных инвестиций, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном решении занятых клеток было m+n- 1.
· Прирост эффективности (изменение целевой функции) при переходе к новому базисному решению зависит от оценки свободной клетки 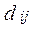 и значения параметра
и значения параметра 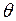 :
: 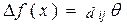 .
.
100–   (1,2) (1,2) |  + + (1,3) (1,3) |
 10+ 10+ (2,2) (2,2) | 140– (2,3) (2,3) |
Как видно из предыдущего цикла, имеем:
· Свободная клетка (1,3).
· Составили цикл перераспределения инвестиций для 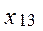 .
.
· При  =100 клетка (1,2) освобождается, а клетка (1,3) становится занятой, получаем новое решение.
=100 клетка (1,2) освобождается, а клетка (1,3) становится занятой, получаем новое решение.
При вычислении оценки 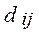 свободной клетки нормативные коэффициенты
свободной клетки нормативные коэффициенты 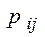 , соответствующие клеткам с +
, соответствующие клеткам с +  , берутся со знаком «+», а клеткам с −
, берутся со знаком «+», а клеткам с −  - со знаком «−» в виде:
- со знаком «−» в виде:
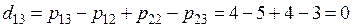 .
.
Тогда приращение целевой функции: 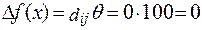 . По циклу некоторое количество инвестиций 1-го инвестора направляется на выполнение 3-го проекта
. По циклу некоторое количество инвестиций 1-го инвестора направляется на выполнение 3-го проекта  , уменьшая количество инвестиций на такую же величину.
, уменьшая количество инвестиций на такую же величину.
Рассмотрим теперь модифицированный метод потенциалов для данного примера.
1 итерация. Вычислим оценки свободных клеток 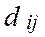 относительно текущего базиса
относительно текущего базиса
| Базисное решение: 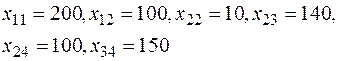 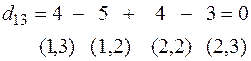 Экономический смысл использования нормативных коэффициентов эффективности: положительные слагаемые оценок соответствуют вершинам цикла, отмеченным параметром (+ Экономический смысл использования нормативных коэффициентов эффективности: положительные слагаемые оценок соответствуют вершинам цикла, отмеченным параметром (+ ), они увеличивают эффект от вложения инвестиций, а отрицательные - параметром (– ), они увеличивают эффект от вложения инвестиций, а отрицательные - параметром (– ), они уменьшают эффект инвестиций ), они уменьшают эффект инвестиций |
Далее рассмотрим циклы перераспределения для других клеток:
| 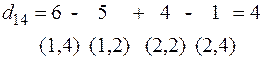 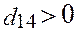 | ||||||||||||||||||||
| 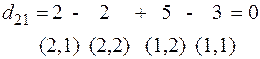 |
| 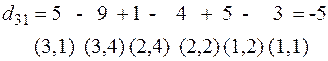 | ||||||||||||||||||||
| 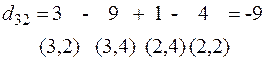 | ||||||||||||||||||||
| 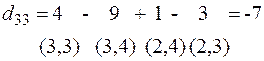 |
Среди вычисленных оценок есть положительная: 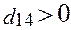 , т.е. исходное решение не оптимальное:
, т.е. исходное решение не оптимальное:
| − | − | |||
| _ | ||||
| _ | _ | _ | ||
Положительную оценку имеет 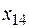 или клетка (1,4). Для перехода к новому базисному решению построим цикл перераспределения инвестиций для (1,4). Находим
или клетка (1,4). Для перехода к новому базисному решению построим цикл перераспределения инвестиций для (1,4). Находим  =min
=min 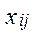 , где
, где 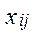 - инвестиции, стоящие в вершинах цикла, отмеченных знаком «–».
- инвестиции, стоящие в вершинах цикла, отмеченных знаком «–».  =min
=min 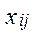 =min(100,100)=100:
=min(100,100)=100:
100 –  +
+ 


 (1,2) (1,4)
(1,2) (1,4)
 |
(2,2) (2,4)
10+  100-
100- 
При  = 100 две базисные переменные
= 100 две базисные переменные 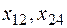 становятся равными нулю:
становятся равными нулю: 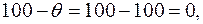 т.е.
т.е. 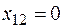 ;
; 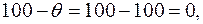 т.е.
т.е. 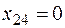 .
.
Тогда новое допустимое базисное решение на первой итерации имеет вид (количество занятых клеток m+n -1=6): 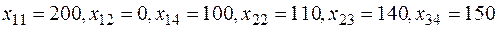 . Нулевое базисное решение
. Нулевое базисное решение 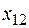 обозначено в таблице как
обозначено в таблице как 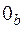 . Переменная
. Переменная 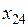 имеет меньший нормативный коэффициент, чем переменная
имеет меньший нормативный коэффициент, чем переменная 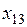
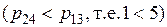 , поэтому
, поэтому 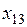 включается в состав базиса, а
включается в состав базиса, а 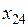 остается небазисной.
остается небазисной.
Таблица 6
 300 300 | 200 3 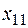 | 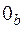 5 5 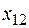 | _ 4 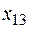 | 100 6 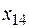 |
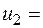 250 250 | _ 2 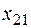 | 110 4 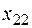 | 140 3 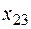 | _ 1 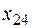 |
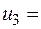 150 150 | _ 5 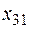 | _ 3 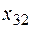 | _ 4 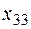 | 150 9 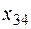 |
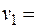 200 200 | 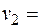 110 110 | 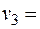 140 140 | 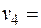 250 250 |
При этом приращение целевой функции равно: 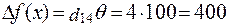 ,
, 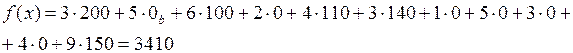
2 итерация. Вычислим оценки свободных клеток 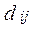 относительно текущего базиса {(1,1),(1,4),(2,2),(2,3),(2,4),(3,4)}.
относительно текущего базиса {(1,1),(1,4),(2,2),(2,3),(2,4),(3,4)}.
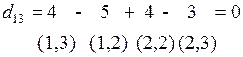
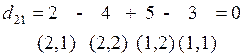
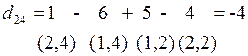
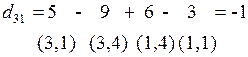
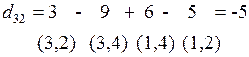
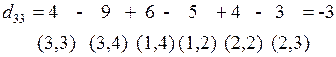
Поскольку оценки 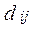 ≤ 0, то решение, полученное в табл. 6 - оптимальное. Таким образом, первое оптимальное решение получено:
≤ 0, то решение, полученное в табл. 6 - оптимальное. Таким образом, первое оптимальное решение получено: 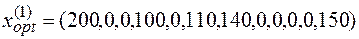 .
.
Замечание. Поскольку имеются нулевые оценки 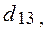
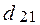 , можем сказать, что оптимальное решение может быть неединственным. В таком случае, во-первых, можно определить всевозможные оптимальные базисные решения и, во-вторых, на их основе сформировать множество оптимальных решений в виде линейной комбинации.
, можем сказать, что оптимальное решение может быть неединственным. В таком случае, во-первых, можно определить всевозможные оптимальные базисные решения и, во-вторых, на их основе сформировать множество оптимальных решений в виде линейной комбинации.
 2015-09-06
2015-09-06 1492
1492
 _
_ 

 +
+ 
 100 _
100 _  +
+  10 +
10 + 
 200 _
200 _  100 +
100 +  +
+ 
 200 _
200 _  100 +
100 +  __
__  +
+  +
+  _
_  +
+  +
+ 
 _
_  +
+  +
+ 






