Теорема. Численность булеана 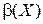 множества X равна двойке, возведенной в степень, равную численности множества X:
множества X равна двойке, возведенной в степень, равную численности множества X:
(6) 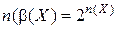 .
.
Каждое подмножество можно выразить индексным кодом — кодовым словом длины n (X), в котором k -й символ является индексом вхождения элемента xk в данное подмножество. Индекс 1, если xk принадлежит подмножеству; индекс 0, если нет. Так коду 000…0 соответствует пустое подмножество, коду 01010…0 — подмножество 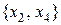 .
.
Очевидно взаимно однозначное соответствие подмножеств и индексных кодов, значит количество подмножеств равно количеству кодов длины n из алфавита {0; 1}. Таких кодов 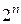 . Значит
. Значит 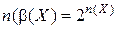 .
.
 2015-09-06
2015-09-06 162
162








