Кинематика

МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА

Контрольные задания для студентов всех специальностей

Красноярск

УДК [531+533] (076)

ББК 22.2

Механика и молекулярная физика: Контрольные задания для студентов всех специальностей / КрасГАСА. Красноярск, 2004.

Составили

А. Е. Бурученко

А. А. Колесников

В. А. Захарова

С.С. Лаптев

О.П. Арнольд

Г.Н. Харук

П.П. Машков

Печатается по решению редакционно-издательского совета академии

Ó Красноярская государственная архитектурно-строительная академия, 2004

ВВЕДЕНИЕ

Физика – фундаментальная база для теоретической подготовки инженеров, без овладения которой их успешная деятельность невозможна.

На всех этапах обучения большое значение имеет практическое применение теоретических знаний в процессе решения задач. Это способствует приобщению студентов к самостоятельной творческой работе, учит анализировать изучаемые явления, выделять главные факторы, отвлекаясь от случайных и несущественных деталей.

Задачи, приведенные в методических указаниях, соответствуют программе общего курса физики в техническом вузе и охватывают разделы «Механика», «Колебания и волны», «Молекулярная физика» и «Термодинамика».

В работе отсутствуют сведения, которые при необходимости могут быть найдены в учебных пособиях по курсу общей физики (см. библиографический список). Поэтому вначале помещен краткий перечень формул и законов, необходимых для решения задач.

В приложении приведены основные справочные данные, дополняющие условия задач. Номера вариантов, которые должен выполнить студент, указывает преподаватель.

ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ

1.1. ОСНОВНЫЕ ФОРМУЛЫ И ЗАКОНЫ

Кинематика

Положение материальной точки в пространстве задаётся радиус-вектором :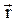

,

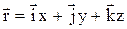где 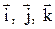– единичные векторы направлений (орты); x, y, z – координаты точки.

Кинематические уравнения движения (в координатной форме) таковы:

; ; ,

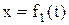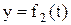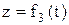где t – время.

Средняя скорость –

< >= ,

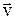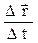где 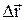– перемещение материальной точки за интервал времени .

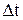Средняя путевая скорость –

< >= ,

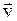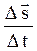где 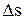- путь, пройденный точкой за интервал времени .

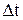Мгновенная скорость –

,

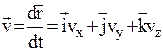где 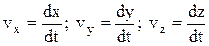– проекции скорости 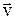на оси координат.

Абсолютное значение скорости –

.

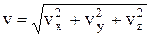Ускорение –

,

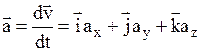где 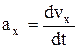; ; 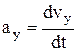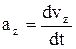– проекции ускорения 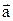на оси координат.

Абсолютное значение ускорения –

.

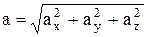При криволинейном движении ускорение можно представить как сумму нормальной 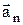и тангенциальной 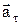составляющих, см. рис 1

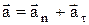
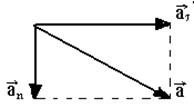Рис. 1.

Абсолютное значение этих ускорений – 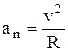; ; 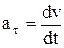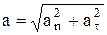, где R – радиус кривизны в данной точке траектории.

Кинематическое уравнение равнопеременного движения материальной точки вдоль оси x:

,

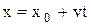где 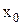- начальная координата; t – время.

При равномерном движении

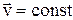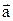; = 0.

Кинематическое уравнение равнопеременного движения (a=const) вдоль оси x:

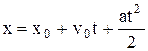
где 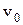– начальная скорость; t – время.

Скорость точки при равномерном движении:

.

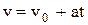Кинематическое уравнение вращательного движения:

.

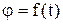Средняя угловая скорость –

,

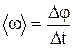где 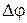- изменение угла поворота за интервал времени .

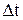Мгновенная угловая скорость –

.

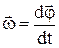Угловое ускорение –

.

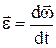Кинематическое уравнение равномерного вращения –

,

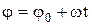где 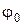- угловое перемещение; t – время. При равномерном вращении

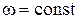и ε=0.

Частота вращения –

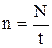, или ,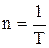

где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота).

Кинематическое уравнение равнопеременного вращения (ε=const):

,

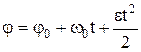где 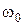- начальная скорость; t – время.

Угловая скорость тела при равнопеременном вращении:

.

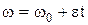Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

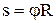(где 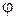– угол поворота тела) – длина пути, пройденного точкой по дуге окружности радиусом R;

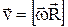, – линейная скорость точки;

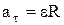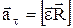, – тангенциальное ускорение точки;

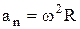– нормальное ускорение точки.