2015-09-06
825
Основное уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси –
,
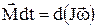где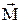 
– момент силы, действующей на тело в течение времени dt; J – момент инерции тела; 
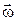– угловая скорость; J 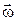– момент импульса.
Если момент силы и момент инерции постоянны, то это уравнение записывается в виде
.
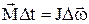В случае постоянного момента инерции
,
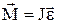где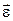 
- угловое ускорение.
Момент силы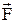 
, действующей на тело, относительно оси вращения –
,
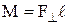где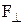 
– проекция силы 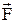на плоскость, перпендикулярную оси вращения; 
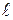– плечо силы (кратчайшее расстояние от оси вращения до линии действия силы).
Момент инерции материальной точки –
,
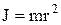где m – масса точки; r – расстояние от оси вращения до точки.
Моменты инерций некоторых тел правильной геометрической формы приведены в табл. 1.
Таблица 1
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой m и длиной 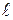| Проходит через центр тяжести стержня перпендикулярно ему Проходит через конец стержня перпендикулярно ему |   |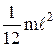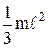
| Тонкое кольцо, обруч, труба радиусом R и массой m, распределённой по ободу | Проходит через центр кольца, обруча, трубы, маховика перпендикулярно плоскости основаня |  |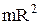
| Круглый однородный диск (цилиндр) радиусом R и массой m | Проходит через центр диска перпендикулярно его плоскости |  |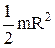
| Однородный шар массой m и радиусом R | Проходит через центр шара |  |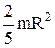
Момент инерции твёрдого тела –
,
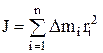где ri – расстояние от элемента массы Dmi до оси вращения.
В интегральной форме это выглядит так:
.
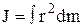Если тело однородно, т. е. его плотность ρ одинаково по всему объёму, то
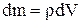и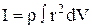 
,
где V – объём тела.
Теорема Штейнера. Момент инерции тела относительно произвольной оси равен
,
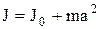где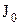 
– момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; m – масса тела; a – расстояние между осями.
Закон сохранения момента импульса –
,
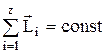где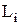 
- момент импульса тела под номером i, входящего в состав системы.
Закон сохранения момента импульса для двух взаимодействующих тел –
,
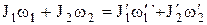где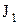 
, 
, 
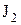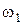и 
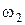- моменты инерции и угловые скорости тел до взаимодействия; 
, 
, 
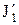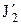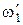и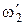 
- те же величины после него.
Закон сохранения момента импульса для одного тела, момент инерции которого меняется, –
,
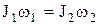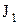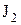где и – начальный и конечный моменты инерци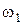и; и 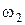– начальная и конечная угловые скорости тела.
Работа постоянного момента силы M, действующего на вращающееся тело, –
,
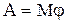где φ – угол поворота тела.
Мгновенная мощность, развиваемая при вращении тела –
.
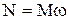Кинетическая энергия вращающегося тела –
.
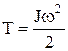Кинетическая энергия тела, катящегося по плоскости без скольжения, –
,
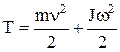где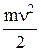 
– кинетическая энергия поступательного движения тела; 
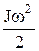– кинетическая энергия вращательного движения вокруг оси, проходящей через центр инерции.
Работа, совершаемая при вращении тела, и изменение его кинетической энергии связаны соотношением
.
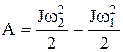Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения (см. табл. 2).
Таблица 2
| Поступательное движение | Вращательное движение | Поступательное движение | Вращательное движение | ||
| Основной закон динамики | Работа и мощность | ||||
  |   |   | | ||
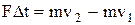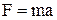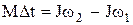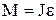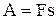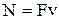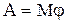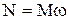| Закон сохранения | Кинетическая энергия | ||||
| импульса | момента импульса |  |  | ||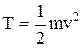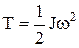
 |  | ||||
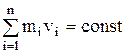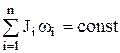Относительное продольное растяжение (сжатие):
,
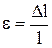где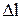 
– изменение длины тела при растяжении (сжатии); l – длина тела до деформации.
Относительное поперечное растяжение (сжатие):
,
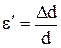где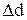 
– изменение диаметра стержня при растяжении (сжатии); d – диаметр стержня.
Связь между относительным поперечным (растяжением) сжатием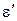 
и относительным продольным растяжением (сжатием) ε –
,
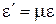где µ – коэффициент Пуассона.
Закон Гука для продольного растяжения (сжатия):
,
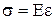где Е – модуль Юнга.
Напряжение упругой деформации –
,
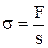где F – растягивающая (сжимающая) сила; s – площадь поперечного сечения.
Потенциальная энергия упругорастянутого (сжатого) стержня –
,
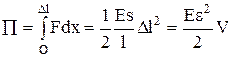где V – объём тела.
