Законы коммутации

1-й закон: Потокосцепление скачком измениться не может:

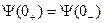
Следствие: В первый момент после коммутации ток в катушке индуктивности скачком измениться не может

.

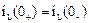2-й закон: Заряд ёмкости скачком измениться не может:

q(0₊) = q(0_-).

Следствие: В первый момент после коммутации напряжение на ёмкости скачком измениться не может

.

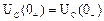На основании законов коммутации определяется постоянная интегрирования свободной составляющей тока или напряжения при расчете переходных процессов. За начало отсчета переходного процесса принимается время равное нулю.

Анализ переходных процессов в линейных цепях с сосредоточенными параметрами сводится к решению линейных неоднородных дифференциальных уравнений, составленных на основе законов Кирхгофа для после коммутационного процесса.

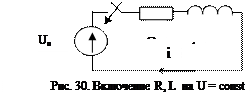
При включении цепи R, L на постоянное напряжение (рис.30):

.

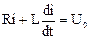Общее решение такого уравнения может быть найдено методом наложения принуждённого и свободного режимов:

; ,

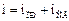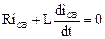где 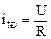- ток принуждённого режима при 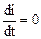или частное решение неоднородного уравнения. Принуждённый режим определяет новое состояние электрической цепи после окончания переходного процесса;

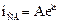- ток свободного режима или общее решение однородного уравнения (с нулевой правой частью).

До коммутации (до включения) ток в цепи отсутствовал 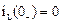. На основании 1-го закона коммутации можно записать 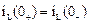, т.е. ток в индуктивности в первый момент после коммутации равен току до коммутации. После коммутации переходный процесс описывается дифференциальным уравнением 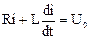. Свободную составляющую определяем из уравнения 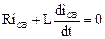. Решение этого уравнения ;

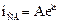k - корень характеристического уравнения ;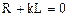

где ;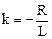

А - постоянная интегрирования, определяемая из начальных условий при t = 0 на основании Первого закона коммутации ,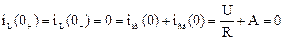

, отсюда .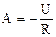

Решение:

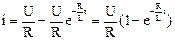
Напряжение на R: .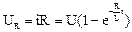

Напряжение на L: .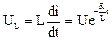

Кривые тока и напряжения на индуктивности при включении R, L на U=const приведены на рис.31.

При включении цепочки R, C на постоянное напряжение (рис.32) уравнение переходного процесса примет вид:

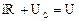, где .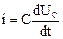

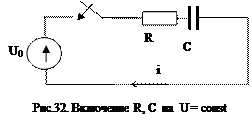После подстановки получим выражение 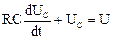. Решим уравнение относительно U_C:

; ; .

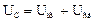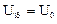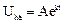Докоммутационный режим 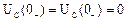. Характеристическое уравнение ; .

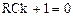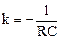А - постоянная интегрирования, определяемая из начальных условий при t = 0:

.

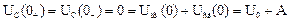Отсюда .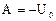

Решение: 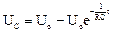и .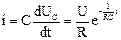

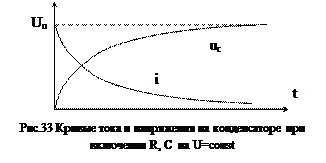Кривые тока и напряжения на конденсаторе при включении R, С на U=const приведены на рис. 33.