2015-09-06
4978
Запишем уравнение Менделеева-Клапейрона:
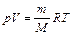, (2.3)
где R - газовая постоянная;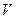 
- объем газа; 
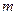- масса газа; 
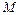- молярная масса газа; 
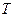- термодинамическая температура газа.
Постоянная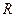 
одинакова для всех газов. Выразим ее из (2.3):
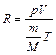, (2.4)
где 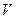- объем воздуха в колбе вместе с подводящими трубками при комнатной температуре.
Объем легко вычислить, если рассмотреть уравнение Менделеева-Клапейрона для двух различных состояний газа:
· при комнатной температуре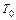 
: 
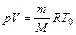(2.4)
· при температуре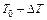 
: 
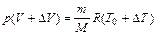. (2.5)
Поделив уравнение (2.5) на уравнение (2.4), получим: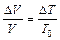 
, откуда объем V газа равен:
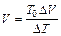. (2.6)
Учитывая, что масса газа может быть найдена как произведение плотности воздуха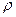 
на объем 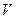, окончательно получим:
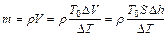, (2.7)
где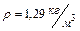 
; 
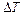- приращение температуры, выбранное экспериментатором.
Так как нагрев воздуха происходит при постоянном давлении, то, продифференцировав уравнение Менделеева-Клапейрона по объему, получим:
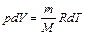, откуда 
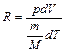(2.8)
Газоваяпостоянная R численно равна работе одного моля газа при изобарном нагревании его на один градус. Следовательно, зная работу расширения газа можно найти постоянную 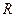из соотношения (2.8). Однако в нашей работе, чтобы исключить ошибки при измерениях 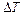и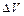 
рекомендуется определить газовую постоянную при исследовании зависимости изменения объема газа от температуры 
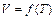, которая представляет собой уравнение Менделеева-Клапейрона, записанное в виде:
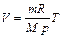(2.9)
Величина, равная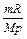 
, является постоянной в данной лабораторной работе. Введем обозначение:
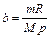, (2.10)
где 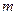- масса газа, найденная ранее, 
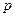- атмосферное давление.
Выразим из (2.10) газовую постоянную R:
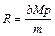, (2.11)
Учитывая (2.10), выражение (2.9) можно представить в виде:
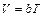(2.12)
Выражение (2.12) представляет собой уравнение прямой, для которой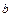 
- угловой коэффициент.
Таким образом, построив по экспериментальным данным график зависимости объема 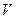от температуры 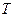можно определить значение углового коэффициента 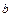, равного тангенсу угла наклона, а затем, используя выражение (2.11) рассчитать значение газовой постоянной R.
