До середніх структурних відносяться дві величини, які називаються "мода" і "медіана".
Мода (модальна величина) ряду – це така величина, яка найбільш часто зустрічається в даному розподілі.
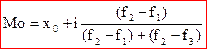
x0 – це нижня межа модального інтервалу.
i – величина інтервалу.
f2 – частота модального інтервалу,
f1 – частота передмодального інтервалу (того, що передує модальному)
f3 – частота позамодального інтервалу (того, що йде після модального інтервалу)
Розрахуймо моду до прикладу №2.
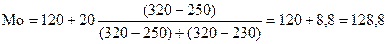
Медіаною називається така величина, що займає серединне положення у варіаційному ряду, в якому варіанти розташовані в зростаючому або спадаючому порядку.
Для дискретного ряду: 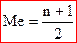
Для варіаційного ряду (приклад №2): 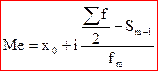
x0 – це нижня межа медіального інтервалу.
i – величина інтервалу.
Sm-1 – сума накопичених частот до медіанного інтервалу.
fm – частота медіанного інтервалу.
| Групування робітників за розміром зарплати (x) | Кількість робітників (f) | Середини інтервалу | Фонд заробітної плати | Наростаючий підсумок частот (накопичені частки) |
| До 100 | ||||
| 100 – 120 | ||||
| 120 – 140 | ||||
| 140 – 160 | ||||
| Понад 160 | ||||
| Разом |
(синім позначено медіанний інтервал: серединою кількості робітників є 500, і він належить до накопиченої частки у третьому ряду)
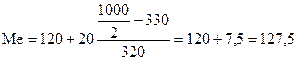
Структурні величини мода і медіана застосовуються для вивчення внутрішньої будови рядів розподілу, тобто їх структури.
 2015-09-06
2015-09-06 241
241








