| Фірми | Вихідні дані | Розрахункові дані | |
| Середня зарплата на 1 робітника, грн. | Фонд заробітної плати, тис. грн. | Середня кількість робітників, чол. | |
| Разом |
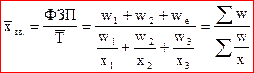
де x – середня кількість робітників, w – середня заробітна плата.
Середня гармонійна зважена застосовується тоді, коли ми маємо загальний обсяг і індивідуальні значення, але не маємо кількості індивідуальних значень.
Приклад. Використання середньої гармонічної. Автомобіль проїхав певну відстань (візьмемо її за 1) зі швидкістю 40 км/год. Назад він повертався зі швидкістю 60 км/год. Яка ж його середня швидкість?
Для розрахунку використаємо середню гармонічну просту:
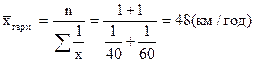
Середня гармонічна – це обернена величина до середньої арифметичної, обчислена з обернених величин осереднюваних варіруючих ознак.
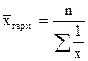
Середні поділяються на 2 великі класи: структурні і степеневі (сюди належать середня гармонічна, середня геометрична, середня квадратична, середня прогресивна тощо).
Середня геометрична розраховується за формулою: 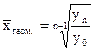
Приклад. Використання середньої арифметичної для розрахунку недискретного ряду.
| Групування робітників за розміром зарплати | Кількість робітників | Фонд заробітної плати |
| До 100 | ||
| 100 – 120 | ||
| 120 – 140 | ||
| 140 – 160 | ||
| Понад 160 | ||
| Разом |
Необхідно знайти середню заробітну плату робітників.
Перш за все ми повинні закрити верхні і нижні границі. Оскільки величина інтервалу в подальших групах дорівнює 20 од., перший інтервал записуємо "80 – 100", останній – "160-180".
Потім знайдемо середину інтервалу:
| Групування робітників за розміром зарплати (x) | Кількість робітників (f) | Середини інтервалу | Фонд заробітної плати |
| До 100 | |||
| 100 – 120 | |||
| 120 – 140 | |||
| 140 – 160 | |||
| Понад 160 | |||
| Разом |
Тоді середня арифметична зважена:
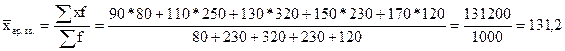
 2015-09-06
2015-09-06 393
393








